Many applications in science, engineering, and modern technology require the solution of boundary value problems for genuine three-dimensional objects. These objects often are of or can be approximated by, an ellipsoidal shape, where the three ellipsoidal semiaxes correspond to three independent degrees of freedom. The triaxial ellipsoid represents the sphere of any anisotropic space and for this reason, it appears naturally in many scientific disciplines. Consequently, despite the complications of the ellipsoidal geometry and mainly its analysis, based on the theory of ellipsoidal harmonics, a lot of progress has been made in the solution of ellipsoidal boundary value problems, due to its general applicability. In this mini-review, we aim to present to the scientific community the main achievements towards the investigation of three such physical problems of medical, engineering and technological significance, those comprising intense research in (a) electroencephalography (EEG) and magnetoencephalography (MEG), (b) creeping hydrodynamics (Stokes flow) and (c) identification of metallic impenetrable bodies, either embedded within the Earth’s conductive subsurface or located into a lossless air environment. In this context, special expertise and particular skills are needed in solving open boundary value problems that incorporate the ellipsoidal geometry and the related harmonic analysis, revealing the fact that there still exists the necessity of involving with these issues.
The ellipsoidal coordinates with its analytical counterparts [11Dassios G. Ellipsoidal harmonics: theory and applications. Cambridge: Cambridge University Press; 2012.-44Hobson EW. The theory of spherical and ellipsoidal harmonics. New York: Chelsea Publishing Company; 1965.] provide the most general system for which the Laplace equation is separable. In this connection, efforts for finding and studying the ellipsoidal harmonics have a long and illustrious history, which spans more than one and a half centuries. The existence, completeness, and orthogonality of the ellipsoidal harmonics were finally proved in 1927 by Moglich in a manuscript 125 pages long. Although the basic theory of ellipsoidal harmonics was completed during the decade of 1930, it is only in the last few years that basic quantitative questions concerning the form of the ellipsoidal harmonics and of the Lamé products were answered, while some of them remain unanswered. The internal ellipsoidal harmonics of degrees 0,1,2 and 3 can be written in closed form. However, the harmonics of degree greater than 3 contain constants, which satisfy polynomial equations of degree more than 5 and Galois theory implies that such roots cannot be found explicitly. Though, specific forms for ellipsoidal harmonics of degrees 5,6, and 7 have been recently discovered [55Dassios G, Satrazemi K. Lamé functions and ellipsoidal harmonics up to degree seven. Int J Spec Funct Appl. 2014;2(1):27-40.]. Furthermore, none of the external ellipsoidal harmonics can be written in closed form, since they are expressed through elliptic integrals. As a result of these complications, there exist ellipsoidal problems in physics, engineering, and modern technology areas remain unsolved, even though many of them have been dealt with satisfactorily. As far as the complete theoretical progress in the field is concerned, it is worth mentioning that much work has been done in both analytical [66Dassios G, Kariotou F, Vafeas P. Invariant vector harmonics: the ellipsoidal case. J Math Anal Appl. 2013;405:652-60.] and computational [77Fragoyiannis G, Vafeas P, Dassios G. On the reducibility of the ellipsoidal system. Math Methods Appl Sci. 2022;45:4497-4554.] levels.
The ellipsoidal geometry provides the most general environment for the study of the anisotropy of the three-dimensional space. Indeed, a scaling of a sphere leads to an ellipsoid, and a particular scaling of an ellipsoid reconstructs the sphere. Consequently, the ellipsoid represents the sphere of any anisotropic space. This generic feature of the ellipsoid explains the ubiquitous nature of ellipsoidal boundary value problems. Bearing in mind this feature, the novelty of any general treatment of the ellipsoidal harmonics and their reductions provides the perfect environment for the construction of several ready-to-use formulae, which can be used in a wide range of applications. Regarding the development of reduction techniques, let us note that this is an important task since, this is not only a means of checking the correctness of the ellipsoidal results, but also provides an opportunity to study the transition process from the 3D ellipsoidal environment to the 2D spheroidal and 1D spherical cases.
The purely ellipsoidal expressions are not easy to handle, thus the results are given in the more tractable form, where Cartesian coordinates are used for the interior harmonics and the standard elliptic integrals are used in the exterior Lamé products. Of course, the harmonic character of the expressions is retained and a mixed Cartesian and ellipsoidal form is obtained. Many relations involving the constants of the ellipsoidal harmonics, as well as relations among the elliptic integrals, are obtained to bring the formulae into their final useful form. The particular way that the elliptic integrals are related is utilized to find useful expressions transforming the Cartesian to the ellipsoidal system and vice versa, wherein this task demands long and tedious analytical calculations. The reduction of ellipsoidal results to corresponding spherical ones is not a straightforward task because the usual limiting rules (such as L’ Hospital rules, etc.) fail. This is because the focal set of the ellipsoidal system is a two-dimensional manifold, i.e., a focal ellipse, while that for the prolate spheroid is a one-dimensional manifold, i.e., a focal segment, and that for the sphere is the center itself (0D manifold). Based on several existing reduction formulae, specific terms can be grouped and appropriate algebraic manipulations can be performed before the limits are taken.
Most of the works concerning important applications in science and modern technology are mainly based on spherical, spheroidal geometry, and other geometries. In this concept, we refer for instance to some selected researches from the literature in the three basic physical areas of consideration, those being Electroencephalography (EEG) and Magnetoencephalography (MEG) (e.g., see [88Kariotou F. On the mathematics of EEG and MEG in spheroidal geometry. Bull Greek Math Soc. 2003;47:117-35.-1010Dassios G, Doschoris M, Satrazemi K. Localizing brain activity from multiple distinct sources via EEG. J Appl Math. 2014;2014:232747.] for forward problems, [1111Dassios G, Hadjiloizi D. On the non-uniqueness of the inverse problem associated with electroencephalography. Inverse Problems. 2009;25:115012.-1414Dassios G, Doschoris M, Satrazemi K. On the resolution of synchronous dipolar excitations via MEG measurements. Q Appl Math. 2018;76:39-45.] for inverse problems and [1515Doschoris M, Dassios G, Fragoyiannis G. Sensitivity analysis of the forward electroencephalographic problem depending on head shape variations. Math Probl Eng. 2015;2015:1-14.-1818Papargiri A, Kalantonis VS, Fragoyiannis G. Mathematical modeling of brain swelling in electroencephalography and magnetoencephalography. Mathematics. 2023;11:2582.] for head shape variations), Stokes creeping flow hydrodynamics (e.g., see [1919Dassios G, Vafeas P. Connection formulae for differential representations in Stokes flow. J Comput Appl Math. 2001;133:283-94.,2020Dassios G, Vafeas P. The 3D Happel model for complete isotropic Stokes flow. Int J Math Math Sci. 2004;46:2429-41.] for spherical flows [2121Dassios G, Vafeas P. On the spheroidal semiseparation for Stokes flow. Res Lett Phys. 2008;2008:135289:1-4.,2222Vafeas P, Protopapas E, Hadjinicolaou M. On the analytical solution of the Kuwabara-type particle-in-cell model for the non-axisymmetric spheroidal Stokes flow via the Papkovich - Neuber representation. Symmetry. 2022;14:170:1-21.], for spheroidal flows and [2323Svarnas P, Papadopoulos PK, Vafeas P, Gkelios A, Clément F, Mavon A. Influence of atmospheric pressure guided streamers (plasma bullets) on the working gas pattern in air. IEEE Trans Plasma Sci. 2014;42:2430-1.-2525Vafeas P, Bakalis P, Papadopoulos PK. Effect of the magnetic field on the ferrofluid flow in a curved cylindrical annular duct. Phys Fluids. 2019;31:117105:1-15.] for circular cylindrical flows) and identification of metallic bodies in either conductive or lossless media (e.g., see [2626Vafeas P, Perrusson G, Lesselier D. Low-frequency solution for a perfectly conducting sphere in a conductive medium with dipolar excitation. Prog Electromagn Res. 2004;49:87-111.-2929Vafeas P, Lesselier D, Kariotou F. Estimates for the low-frequency electromagnetic fields scattered by two adjacent metal spheres in a lossless medium. Math Methods Appl Sci. 2015;38:4210-37.] for scattering from complete isotropic bodies and [3030Vafeas P, Perrusson G, Lesselier D. Low-frequency scattering from perfectly conducting spheroidal bodies in a conductive medium with magnetic dipole excitation. Int J Eng Sci. 2009;47:372-90.-3333Vafeas P. Low-frequency electromagnetic scattering by a metal torus in a lossless medium with magnetic dipolar illumination. Math Methods Appl Sci. 2016;39:4268-92.] for scattering from bodies of different geometry). In this mini-review, we demonstrate the applicability of the analytical results on ellipsoidal harmonics (supplemented by the appropriate numerical calculations) via the introduction of pioneer works, to show that they become effective for solving real-life problems within the frame of the aforementioned physical areas, while any reader can be initiated to solve open problems in the ellipsoidal regime. We emphasize the fact that the coherence between the three aforementioned physical areas is based on the existence of solid bodies (the human head for EEG and MEG, the particles for Stokes creeping hydrodynamic flow, and the voluminous metallic objects for scattering in conductive and lossless media), which can be geometrically represented by a genuine ellipsoid. Furthermore, in the forthcoming paragraphs, we present works that incorporate the appropriately developed mathematical and numerical techniques, which allow us to implement the reduction from the 3D ellipsoidal to the 2D spheroidal and the 1D spherical cases.
Electroencephalography (EEG) and Magnetoencephalography (MEG)
The study of electromagnetic phenomena [3434Stratton JA. Electromagnetic theory. New York: McGraw-Hill; 1941.,3535Maxwell JC. A treatise on electricity and magnetism. Vols. I & II. Oxford: Oxford University Press; 1998.] that occur within the human brain concerns the interdisciplinary field of electromagnetism in biotechnology, which extends from the theoretical branch of mathematics to the more practical area of physics and medicine. Among the most widely used noninvasive methods for studying electromagnetic human brain activity, EEG and MEG [3636Dassios G, Fokas AS. Electroencephalography and magnetoencephalography. Boston: De Gruyter; 2020.,3737Dassios G, Fokas AS. The definite non-uniqueness results for deterministic EEG and MEG data. Inverse Problems. 2013;29:065012.] stand as the most famous and applicable techniques nowadays. On one hand, EEG is the method, according to which the electrochemical activity of the brain is mapped on an electroencephalogram. Therein, the data of EEG are electric potentials registered on the head surface by properly placed electrodes. The electrochemical source generates the externally measured electric potential, which can be calculated provided by a given source and this procedure determines the forward EEG problem. Therein, the interpretation of the EEG data to locate the geometrical and physical characteristics of the source inside the brain identifies the known inverse EEG problem. On the other hand, MEG is the determination of the neuronal current in the brain from measurements outside the brain of the magnetic field generated by the current. The magnetic field is measured by the so-called Super Quantum Interference Device (SQUID), where such devices exists in several brain imaging laboratories. Furthermore, it is notable that MEG is the only existing imaging technique capable of real-time reconstruction. However, MEG is still not widely used due to its poor spatial resolution, however much work has been done towards the improvement of the existing reconstruction techniques with a significant impact on brain imaging.
The physiological basis of EEG and MEG is the following. The main functional units of the brain are certain highly specialized cells that are called neurons. For higher mental processes the most important part of the brain is its outermost layer, called the cerebral cortex, which contains at least 1010 neurons. When neurons are active they produce small currents, whose basis is the change in the concentration of certain ions (ionic currents). The flow of current in the neural system produces an electric field and a weak magnetic field. The measurement of the electric field on the head’s surface is called EEG, while the measurement of the magnetic field outside the brain and the estimation of the current density distribution that produces this field is called MEG. Under the assumption that the space occupied by the brain is approximately a sphere, the part of the current, which can be reconstructed from the measurements, is precisely calculated by inverting the so-called Geselowitz equation. This part consists of only certain moments of one of the two functions specifying the tangential part of the current. The other function, specifying the radial part of the current, is completely arbitrary. However, it is also shown that with the assumption of energy minimization, the current can be reconstructed uniquely. An analogous problem is also investigated under the assumption that the current is a dipole. During the last decade, the already ample literature on EEG and MEG research in the spherical and spheroidal geometry has been enriched and extended with several works by using more realistic models for the brain [3838Dassios G. Electric and magnetic activity of the brain in spherical and ellipsoidal geometry. In: Ammari H, editor. Mathematical modeling in biomedical imaging I. Berlin: Springer. 2009; 133-202.-4040Dassios G, Fokas AS. Electro-magneto-encephalography for a three-shell model: dipoles and beyond for the spherical geometry. Inverse Problems. 2009;25:035001.] (see, also, explicit works on EEG [4141Kariotou F. Electroencephalography in ellipsoidal geometry. J Math Anal Appl. 2004;290:324-42.-4444Doschoris M, Kariotou F. Error analysis for nonconfocal ellipsoidal systems in the forward problem of electroencephalography. Math Methods Appl Sci. 2018;41:6793-813.] and MEG [4545Dassios G, Kariotou F. Magnetoencephalography in ellipsoidal geometry. J Math Phys. 2003;44:220-41.-4747Dassios G, Hadjiloizi D, Kariotou F. The octapolic ellipsoidal term in magnetoencephalography. J Math Phys. 2009;50:013508.]), which is approximated by an ellipsoid and it is also surrounded by the cerebrospinal fluid, the bulk, and the skin.
Stokes creeping flow
In engineering-type analyses, it is not usually necessary to have detailed solutions of the flow field over the entire swarm of particles, since such solutions are cumbersome to use. Thus, the technique of cell models is adopted, where the mathematical treatment of each problem is based on the assumption that a three-dimensional assemblage may be considered to consist of several identical unit cells. Each of these cells contains a particle, surrounded by a fluid envelope and containing a volume of fluid sufficient to make the fractional void volume in the cell equal to that in the entire assemblage. The most widely used and general model considers that the particle is moving and the fluid is stationary, imposing the so-called Happel-type boundary conditions. Here, it is introduced the low Reynolds number flow of a swarm of particles in an otherwise quiescent Newtonian fluid, that moves with constant uniform velocity in an arbitrary direction and rotates with an arbitrary constant angular velocity, inheriting the three-dimensional nature of the phenomenon. Particle-in-cell models for Stokes flow through a homogeneous swarm of particles are of substantial practical interest because they provide a relatively simple platform for the analytical or semi-analytical solution of heat and mass transport problems. For many flow problems involving small particles, spherical and spheroidal geometry provide a good approximation. However, more realistic models involve particles of arbitrary shape, whereas it is almost impossible to take advantage of symmetry. Hence, modern research is concentrated on ellipsoidal geometry, which provides the most widely used framework for representing small particles of arbitrary, non-axisymmetric (3D) shape that are embedded within a fluid that flows according to Stokes law.
In recent days, a complete solution of flow through a swarm of particles is possible with powerful numerical methods, which, however, involve the use of elaborate computer codes. Hence, there exists a continuous need for analytical methods, which capture the essential features of the transport process and provide insight into the associated physical processes, so, under this particular frame, particle-in-cell flow models have been extensively investigated. The cases of axisymmetric shapes (sphere or spheroid) have been extensively investigated and analytical solutions in closed forms have been obtained either directly or using specific techniques. On the other hand, the usefulness of representation theory has been demonstrated by solving three-dimensional sphere-in-cell and spheroid-in-cell Happel models. The spherical approach for such axisymmetric problems has been adopted since 1949 and several complete analytical solutions have been obtained, while later on researchers investigated a 2D spheroid-in-cell instead of a sphere-in-cell model, by introducing a novel method of semi-separation of variables, which is based on an appropriate finite-dimensional spectral decomposition of the operator of motion. These spherical and spheroidal solutions have been validated through the solution of 3D boundary value problems in spherical and spheroidal coordinates, demonstrating the practical efficiency of the differential representations theory. To solve generalized Stokes flow problems in ellipsoidal geometry [4848Vafeas P, Dassios G. Stokes flow in ellipsoidal geometry. J Math Phys. 2006;47:093102:1-38.,4949Hatzikonstantinou PM, Vafeas P. A general theoretical model for the magnetohydrodynamic flow of micropolar magnetic fluids: application to Stokes flow. Math Methods Appl Sci. 2010;33:233-48.], an ellipsoid-in-cell model with Happel-type boundary conditions is assumed, wherein the 3D boundary value problem is solved with the aid of the Papkovich - Neuber complete differential representation of the flow fields for Stokes flow.
Metallic bodies in conductive and lossless media
In recent days, the general theory of electromagnetism and scattering [5050Stratton JA. Electromagnetic theory. New York: McGraw-Hill; 1941.,5151Dassios G, Kleinman RE. Low-frequency scattering. Oxford: Oxford University Press; 2000.] has been used for retrieving an anomaly of some sort, such as metallic bodies, from three-dimensional magnetic fields, which are measured along a borehole with the aid of a low-frequency time-harmonic source. These bodies are considered scatterers and they are usually embedded in either a conductive medium, such as Earth’s subsurface, or a lossless environment, such as air and vacuum cavities. By deciphering the obtained data, one can infer information regarding the orientation, size, shape, and electromagnetic parameters of the anomalies, which comprises the inverse problem [5252Ammari H, Kang H. Polarization and moment tensors: with applications to inverse problems and effective medium theory. Applied Mathematical Sciences. Vol. 162. New York: Springer-Verlag; 2007.], as long as the direct one of calculating the implicated electric and magnetic fields is readily solved. There exist several proposed methodologies in the quite recent bibliography [5353Björkberg J, Kristenson G. Three-dimensional subterranean target identification by use of optimization techniques. Prog Electromagn Res. 1997;15:141-64.-5757Tortel H. Electromagnetic imaging of a three-dimensional perfectly conducting object using a boundary integral formulation. Inverse Problems. 2004;20:385-98.], which provide us with effective techniques to deal with such problems. Nevertheless, beyond this frame, the necessity of closed-form compact solutions, to assist a possible inversion scheme, was inevitable. It is to this end that the low-frequency theory significantly improved the already existing models towards the identification of metallic bodies. Given this aspect, the current investigation concerns the interaction of an arbitrarily orientated, time-harmonic, magnetic dipole with perfectly conducting bodies, which are embedded in homogeneous conductive or lossless media. A rigorous low-frequency expansion of electromagnetic field in positive integral powers of the wavenumber of the exterior medium is constructed and, then the problem is mapped to the solution of the equations of Laplace and Poisson in three-dimensional fields using harmonic functions to represent the electromagnetic fields. It is readily verified numerically that the first four terms are sufficient to provide with great accuracy both the electric and the magnetic fields.
Under the interest of devising simple mathematical and numerical tools to bring insight to the field by solving with reasonable accuracy the direct and the inverse problems, it is important to be capable of solving such situations for as much general geometry of the body as possible. As with these earlier topics, these problems in spherical and spheroidal geometry have been treated extensively, as shown previously. Consequently, the need to solve the same boundary value problems in the low-frequency spectrum, as they are described earlier, but in ellipsoidal coordinates, raised significantly [5858Perrusson G, Vafeas P, Lesselier D. Low-frequency dipolar excitation of a perfect ellipsoidal conductor. Q Appl Math. 2010;68:513-36.-6060Vafeas P. Low-frequency dipolar electromagnetic scattering by a solid ellipsoid in the lossless environment. Stud Appl Math. 2020;145:217-46.]. In such works, a single voluminous anomaly is investigated, described as a triaxial ellipsoid of arbitrary semi-axis orientations, whose conductivity is infinite and which is embedded in a homogeneous medium, which is isotropic, non-magnetic and either conductive or lossless. A magnetic dipole is operated at a given circular frequency at a certain location and radiates primary magnetic and electric fields. It induces secondary magnetic and electric fields, whose magnetic components are either sought or collected along a single line passing outside the body. The formation of the ellipsoidal electromagnetic fields is based on the low-frequency expansion of the incident and the scattered fields in positive integral powers of the wavenumber of the exterior medium. The calculations are restricted to the first three terms of the relevant expansion, being verified analytically and numerically that they provide sufficient accuracy for the entire solution. More specifically, the magnetic field of the third order (the corresponding electric field is equal to zero) is not expected to have a significant contribution, while the magnetic field of the first order is identically equal to zero since there does not exist the corresponding incident (primary field). Thus, the scattering problem is transformed into a succession, one at each of the remaining orders, of possibly coupled boundary value problems satisfying second-order partial differential equations with proper perfectly reflecting boundary conditions at the body surface. Once the direct problem is solved, it is the solution to the inverse problem for the identification of metallic three-dimensional ellipsoidal objects.
Application examples
This section is devoted to the presentation of concrete application examples that demonstrate the practical implementation of the proposed methods, like real-world applications in the currently investigated fields. Such as EEG and MEG, Stokes hydrodynamic flow, and electromagnetic scattering. Towards this direction, we choose three representative scientific works and we briefly summarize an important numerical demonstration for each case under consideration.
Referring to [1717Papargiri A, Kalantonis VS, Vafeas P, Doschoris M, Kariotou F, Fragoyiannis G. On the geometrical perturbation of a three-shell spherical model in electroencephalography. Math Methods Appl Sci. 2022;45:8876-89.], we begin with the introduction of a multilayer model of the brain, in the context of the direct EEG problem, where all the associated boundaries that confine the conductive areas of the cerebrum, the cerebrospinal fluid, the skull, and the skin are considered as smooth surfaces, while the three-shell head system is assumed to be surrounded by the non-conductive air. The main purpose of this analysis is the evaluation of the impact of the electric excitation of the human brain, which is represented by the bipolar current action of a single equivalent dipole source in the inner conductor, on the electric activity on the surface of the human head (Figure 1).
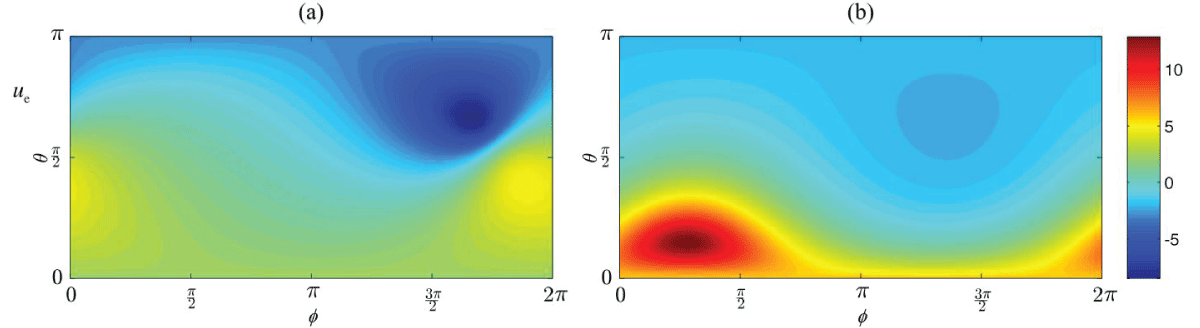Figure 1: The surface potential ue that originates from a three-shell model for an arbitrarily orientated dipole and different dipole settings (a) and (b) for several angles of observation θ and φ.
In the sequel, referring to [2222Vafeas P, Protopapas E, Hadjinicolaou M. On the analytical solution of the Kuwabara-type particle-in-cell model for the non-axisymmetric spheroidal Stokes flow via the Papkovich - Neuber representation. Symmetry. 2022;14:170:1-21.], a methodology for dealing with the problem of Stokes flow through a swarm of particles with Kuwabara-type boundary conditions is developed. The conducted research is based on the reliable particle-in-cell technique by which the creeping flow through the swarm of the particles is modeled as flow within a fluid envelope that surrounds a single solid particle and attains a fictitious boundary expressing this way the disturbance to flow that causes the rest of the particles of the assemblage and the volume of the fluid envelope matches to the fluid volume fraction of the swarm. Hence, given the Kuwabara model that assumes an arbitrarily moving fluid around a motionless particle, the non-slip flow condition on the surface of the inner surface is supplemented by the boundary conditions on the outer surface, i.e. zero normal velocity component and vorticity. Due to the non-axisymmetric nature of the physical problem, the velocity field attains a three-dimensional behavior around the particle, providing an arbitrary fluid motion (Figure 2).
Figure 2: The 3D velocity field v = (v1, v2, v3) in the three-dimensional space (x1, x2, x3).
Finally, referring to [5959Perrusson G, Vafeas P, Chatjigeorgiou IK, Lesselier D. Low-frequency on-site identification of a highly conductive body buried in Earth from a model ellipsoid. IMA J Appl Math. 2015;80:963-80.], a strict low-frequency approximation of the fields that are scattered by an impenetrable metallic body under the influence of a vertical magnetic dipole source enables the development of a reliable scheme of identification of an orebody in the less conductive Earth from data measured on-site. A few in-phase (real) and quadrature (imaginary) three-component field data are enough to achieve a rather robust inversion with a low-complexity inversion algorithm. The approach has the benefit that the assumed body geometry caters to a wide range of orientations, sizes, and shapes. Also, the low-frequency approximation methodology yields both real and imaginary field contributions, which are necessary to achieve proper body identification, being assumed perfectly electrically conducting (Figure 3).
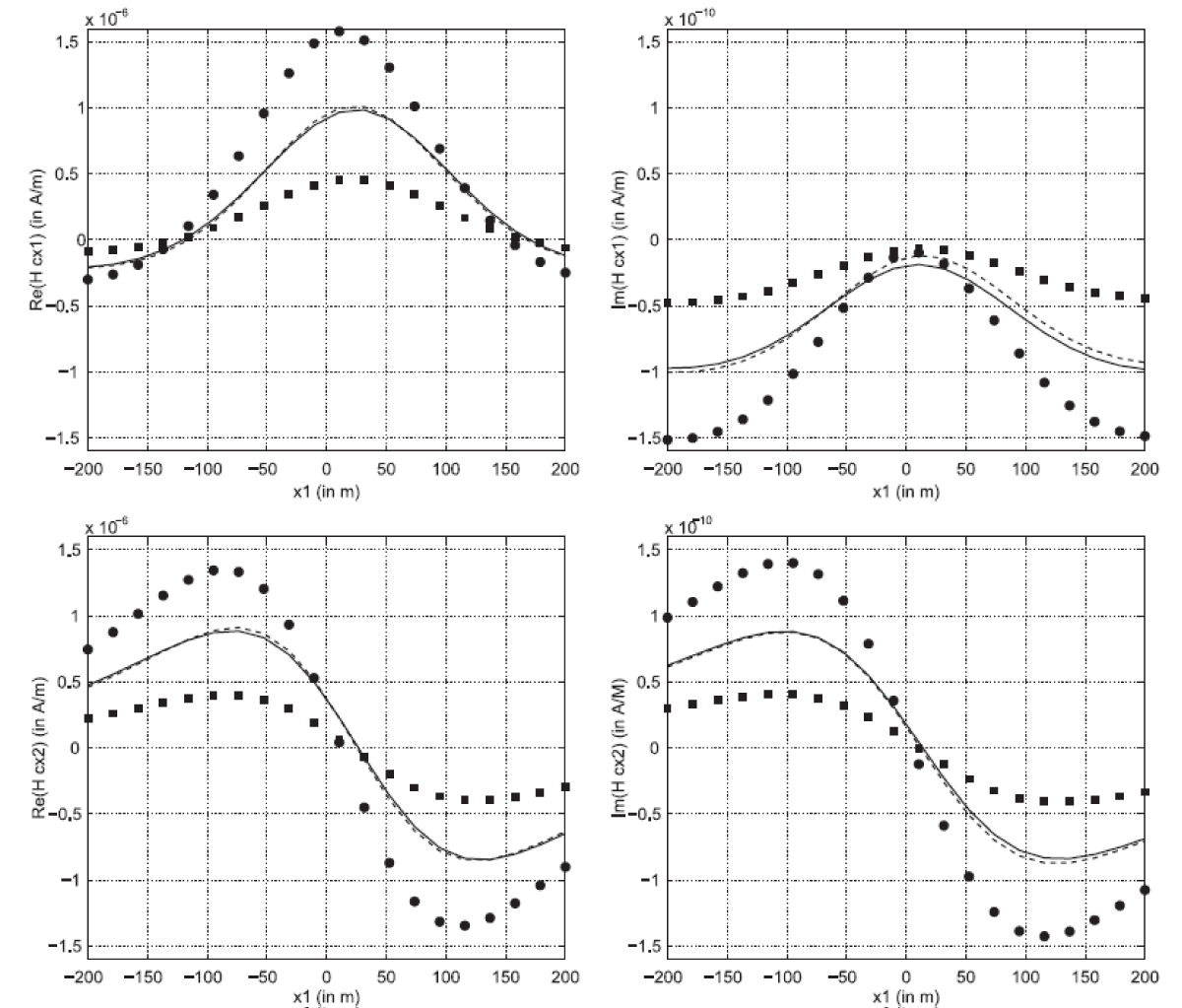Figure 3: Real (left column) and imaginary (right column) parts of the magnetic field scattered by several metallic bodies. The third components all vanish due to the position of the magnetic dipole.
The current mini-review aims to the presentation of the most important research works, which are involved with the solution of several boundary value problems with physical significance that are set in the frame of the three-dimensional ellipsoidal geometry and the corresponding harmonic analysis. Our review, without excluding other possible applications, is restricted to three main physical areas with increasing contributions to modern scientific knowledge, which are the following: (a) Problems arising in electroencephalography (EEG), i.e., recording and analysis of the electrical activity of the brain via electrodes, which are placed on the scalp and then are linked to an electroencephalograph and magnetoencephalography (MEG), i.e., measuring of magnetic signals, using a special device called SQUID (Superconducting Quantum Interference Device) at a specific distance of 3-6cm from the head surface. In both cases, the human brain can be approximated by an ellipsoid with average semiaxes 6, 6.5, and 9 cm. (b) Specific problems concerning particles within Stokes creeping flow fields, wherein the deposition of impurities on the obstacles carried by the continuous flow, reshape the particles in the form of ellipsoids. (c) Applications related to the identification of metallic-type impenetrable objects in either conductive (like Earth’s subsurface) or lossless (like air cavities) environments, using an optimization process, which can be approximated by an ellipsoid.
Dassios G. Ellipsoidal harmonics: theory and applications. Cambridge: Cambridge University Press; 2012.
Moon P, Spencer E. Field theory handbook. Berlin: Springer-Verlag; 1971.
Morse PM, Feshbach H. Methods of theoretical physics. Vols. I & II. New York: McGraw-Hill; 1953.
Hobson EW. The theory of spherical and ellipsoidal harmonics. New York: Chelsea Publishing Company; 1965.
Dassios G, Satrazemi K. Lamé functions and ellipsoidal harmonics up to degree seven. Int J Spec Funct Appl. 2014;2(1):27-40.
Dassios G, Kariotou F, Vafeas P. Invariant vector harmonics: the ellipsoidal case. J Math Anal Appl. 2013;405:652-60.
Fragoyiannis G, Vafeas P, Dassios G. On the reducibility of the ellipsoidal system. Math Methods Appl Sci. 2022;45:4497-4554.
Kariotou F. On the mathematics of EEG and MEG in spheroidal geometry. Bull Greek Math Soc. 2003;47:117-35.
Dassios G, Fokas AS, Hadjiloizi D. On the complementarity of electroencephalography and magnetoencephalography. Inverse Problems. 2007;23:2541.
Dassios G, Doschoris M, Satrazemi K. Localizing brain activity from multiple distinct sources via EEG. J Appl Math. 2014;2014:232747.
Dassios G, Hadjiloizi D. On the non-uniqueness of the inverse problem associated with electroencephalography. Inverse Problems. 2009;25:115012.
Dassios G, Fragoyiannis G, Satrazemi K. On the inverse EEG problem for a 1D current distribution. J Appl Math. 2014;2014:715785.
Dassios G, Satrazemi K. Inversion of electroencephalography data for a 2D current distribution. Math Methods Appl Sci. 2014;38:1098-1105.
Dassios G, Doschoris M, Satrazemi K. On the resolution of synchronous dipolar excitations via MEG measurements. Q Appl Math. 2018;76:39-45.
Doschoris M, Dassios G, Fragoyiannis G. Sensitivity analysis of the forward electroencephalographic problem depending on head shape variations. Math Probl Eng. 2015;2015:1-14.
Doschoris M, Vafeas P, Fragoyiannis G. The influence of surface deformations on the forward magnetoencephalographic problem. SIAM J Appl Math. 2018;78:963-76.
Papargiri A, Kalantonis VS, Vafeas P, Doschoris M, Kariotou F, Fragoyiannis G. On the geometrical perturbation of a three-shell spherical model in electroencephalography. Math Methods Appl Sci. 2022;45:8876-89.
Papargiri A, Kalantonis VS, Fragoyiannis G. Mathematical modeling of brain swelling in electroencephalography and magnetoencephalography. Mathematics. 2023;11:2582.
Dassios G, Vafeas P. Connection formulae for differential representations in Stokes flow. J Comput Appl Math. 2001;133:283-94.
Dassios G, Vafeas P. The 3D Happel model for complete isotropic Stokes flow. Int J Math Math Sci. 2004;46:2429-41.
Dassios G, Vafeas P. On the spheroidal semiseparation for Stokes flow. Res Lett Phys. 2008;2008:135289:1-4.
Vafeas P, Protopapas E, Hadjinicolaou M. On the analytical solution of the Kuwabara-type particle-in-cell model for the non-axisymmetric spheroidal Stokes flow via the Papkovich - Neuber representation. Symmetry. 2022;14:170:1-21.
Svarnas P, Papadopoulos PK, Vafeas P, Gkelios A, Clément F, Mavon A. Influence of atmospheric pressure guided streamers (plasma bullets) on the working gas pattern in air. IEEE Trans Plasma Sci. 2014;42:2430-1.
Vafeas P, Bakalis P, Papadopoulos PK. Effect of the magnetic field on the ferrofluid flow in a curved cylindrical annular duct. Phys Fluids. 2019;31:117105:1-15.
Vafeas P, Perrusson G, Lesselier D. Low-frequency solution for a perfectly conducting sphere in a conductive medium with dipolar excitation. Prog Electromagn Res. 2004;49:87-111.
Stefanidou E, Vafeas P, Kariotou F. An analytical method of electromagnetic wave scattering by a highly conductive sphere in a lossless medium with low-frequency dipolar excitation. Mathematics. 2021;9:3290:1-25.
Vafeas P, Papadopoulos PK, Lesselier D. Electromagnetic low-frequency dipolar excitation of two metal spheres in a conductive medium. J Appl Math. 2012;628261:1-37.
Vafeas P, Lesselier D, Kariotou F. Estimates for the low-frequency electromagnetic fields scattered by two adjacent metal spheres in a lossless medium. Math Methods Appl Sci. 2015;38:4210-37.
Vafeas P, Perrusson G, Lesselier D. Low-frequency scattering from perfectly conducting spheroidal bodies in a conductive medium with magnetic dipole excitation. Int J Eng Sci. 2009;47:372-90.
Vafeas P. Dipolar excitation of a perfectly electrically conducting spheroid in a lossless medium at the low-frequency regime. Adv Math Phys. 2018;9587972:1-20.
Vafeas P, Papadopoulos PK, Ding P-P, Lesselier D. Mathematical and numerical analysis of low-frequency scattering from a PEC ring torus in a conductive medium. Appl Math Model. 2016;40:6477-500.
Vafeas P. Low-frequency electromagnetic scattering by a metal torus in a lossless medium with magnetic dipolar illumination. Math Methods Appl Sci. 2016;39:4268-92.
Stratton JA. Electromagnetic theory. New York: McGraw-Hill; 1941.
Maxwell JC. A treatise on electricity and magnetism. Vols. I & II. Oxford: Oxford University Press; 1998.
Dassios G, Fokas AS. Electroencephalography and magnetoencephalography. Boston: De Gruyter; 2020.
Dassios G, Fokas AS. The definite non-uniqueness results for deterministic EEG and MEG data. Inverse Problems. 2013;29:065012.
Dassios G. Electric and magnetic activity of the brain in spherical and ellipsoidal geometry. In: Ammari H, editor. Mathematical modeling in biomedical imaging I. Berlin: Springer. 2009; 133-202.
Fokas AS. Electro-magneto-encephalography for a three-shell model: distributed current in arbitrary, spherical and ellipsoidal geometries. J R Soc Interface. 2009 May 6;6(34):479-88. doi: 10.1098/rsif.2008.0309. Epub 2008 Aug 29. PMID: 18757270; PMCID: PMC2659695.
Dassios G, Fokas AS. Electro-magneto-encephalography for a three-shell model: dipoles and beyond for the spherical geometry. Inverse Problems. 2009;25:035001.
Kariotou F. Electroencephalography in ellipsoidal geometry. J Math Anal Appl. 2004;290:324-42.
Giapalaki S, Kariotou F. The complete ellipsoidal shell model in EEG imaging. Abstr Appl Anal. 2006;2006:57429.
Doschoris M, Kariotou F. Quantifying errors during the source localization process in electroencephalography for confocal systems. IMA J Appl Math. 2018;83:243-60.
Doschoris M, Kariotou F. Error analysis for nonconfocal ellipsoidal systems in the forward problem of electroencephalography. Math Methods Appl Sci. 2018;41:6793-813.
Dassios G, Kariotou F. Magnetoencephalography in ellipsoidal geometry. J Math Phys. 2003;44:220-41.
Dassios G, Giapalaki SN, Kandili AN, Kariotou F. The exterior magnetic field for the multilayer ellipsoidal model of the brain. Q J Mech Appl Math. 2007;60:1-25.
Dassios G, Hadjiloizi D, Kariotou F. The octapolic ellipsoidal term in magnetoencephalography. J Math Phys. 2009;50:013508.
Vafeas P, Dassios G. Stokes flow in ellipsoidal geometry. J Math Phys. 2006;47:093102:1-38.
Hatzikonstantinou PM, Vafeas P. A general theoretical model for the magnetohydrodynamic flow of micropolar magnetic fluids: application to Stokes flow. Math Methods Appl Sci. 2010;33:233-48.
Stratton JA. Electromagnetic theory. New York: McGraw-Hill; 1941.
Ammari H, Kang H. Polarization and moment tensors: with applications to inverse problems and effective medium theory. Applied Mathematical Sciences. Vol. 162. New York: Springer-Verlag; 2007.
Björkberg J, Kristenson G. Three-dimensional subterranean target identification by use of optimization techniques. Prog Electromagn Res. 1997;15:141-64.
Yu T, Carin L. Analysis of the electromagnetic inductive response of a void in a conducting-soil background. IEEE Trans Geosci Remote Sens. 2000;38:1320-7.
Huang H, Won IJ. Detecting metal objects in magnetic environments using a broadband electromagnetic method. Geophysics. 2003;68:1877-87.
Cui TJ, Chew WC, Wright DL, Smith DV. Three-dimensional imaging for buried objects in a very lossy earth by inversion of VETEM data. IEEE Trans Geosci Remote Sens. 2003;41:2197-210.
Tortel H. Electromagnetic imaging of a three-dimensional perfectly conducting object using a boundary integral formulation. Inverse Problems. 2004;20:385-98.
Perrusson G, Vafeas P, Lesselier D. Low-frequency dipolar excitation of a perfect ellipsoidal conductor. Q Appl Math. 2010;68:513-36.
Perrusson G, Vafeas P, Chatjigeorgiou IK, Lesselier D. Low-frequency on-site identification of a highly conductive body buried in Earth from a model ellipsoid. IMA J Appl Math. 2015;80:963-80.
Vafeas P. Low-frequency dipolar electromagnetic scattering by a solid ellipsoid in the lossless environment. Stud Appl Math. 2020;145:217-46.
Vafeas P. Boundary Value Problems in Ellipsoidal Geometry and Applications. IgMin Res.. October 29, 2024; 2(10): 873-879. IgMin ID: igmin263; DOI:10.61927/igmin263; Available at: igmin.link/p263
Department of Chemical Engineering, University of Patras, 26504 Patras, Greece
Address Correspondence: Panayiotis Vafeas, Department of Chemical Engineering, University of Patras, 26504 Patras, Greece, Email: vafeas@chemeng.upatras.gr
How to cite this article: Vafeas P. Boundary Value Problems in Ellipsoidal Geometry and Applications. IgMin Res.. October 29, 2024; 2(10): 873-879. IgMin ID: igmin263; DOI:10.61927/igmin263; Available at: igmin.link/p263
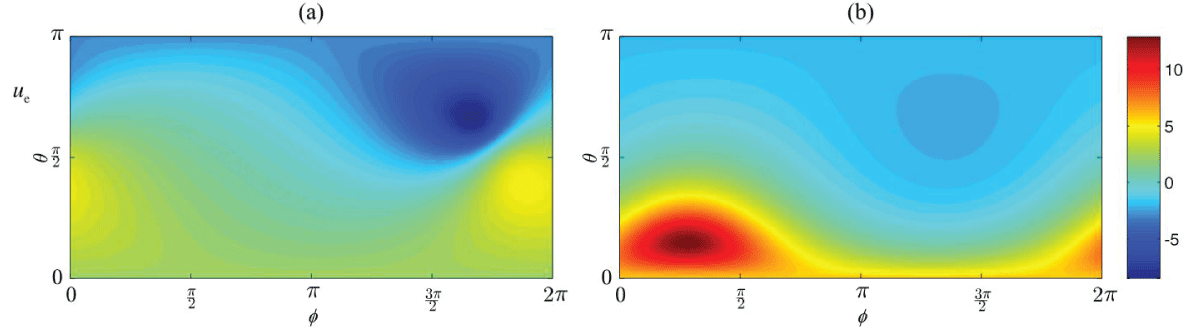Figure 1: The surface potential ue that originates from a th...
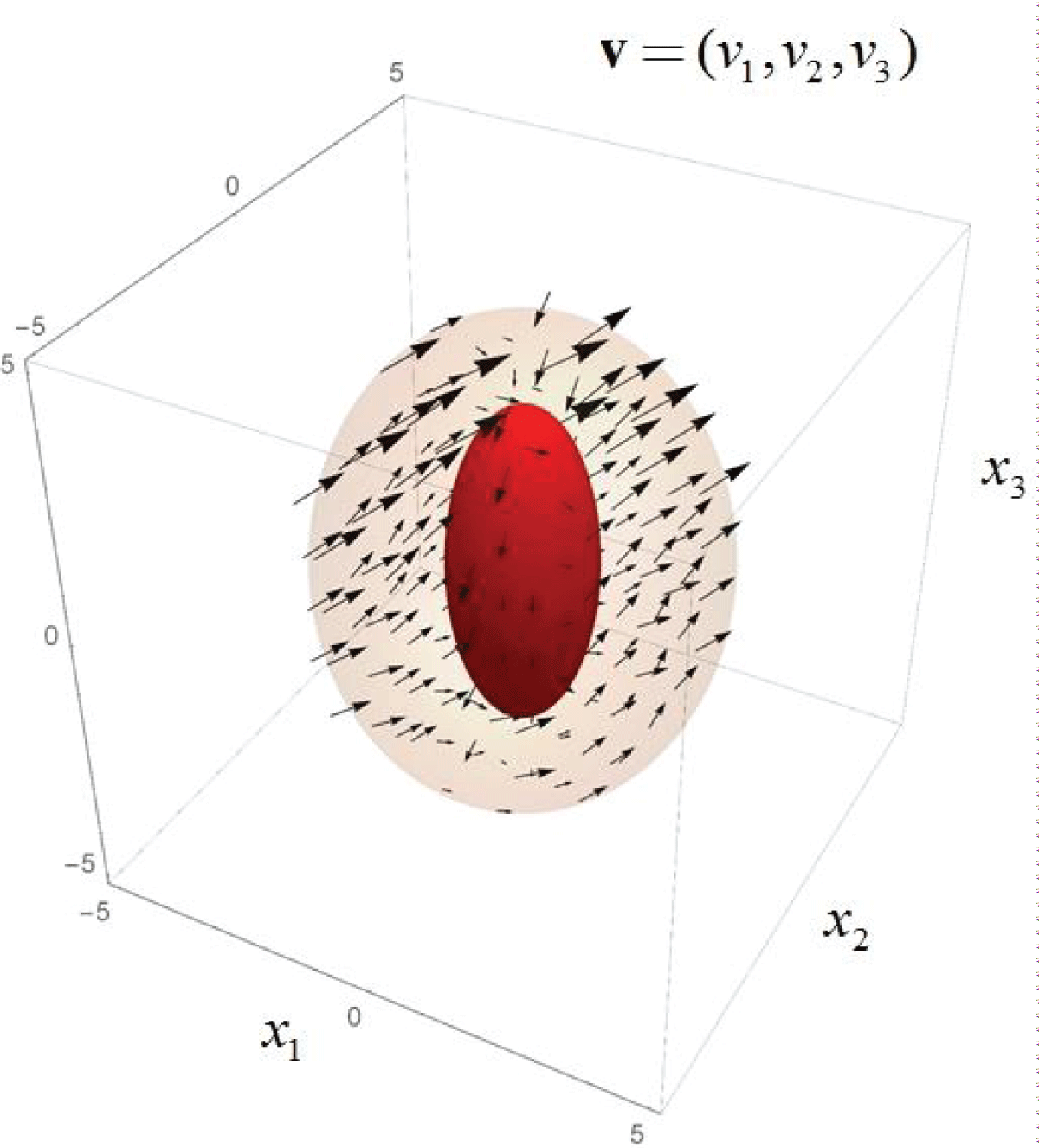Figure 2: The 3D velocity field v = (v1, v2, v3) in the thre...
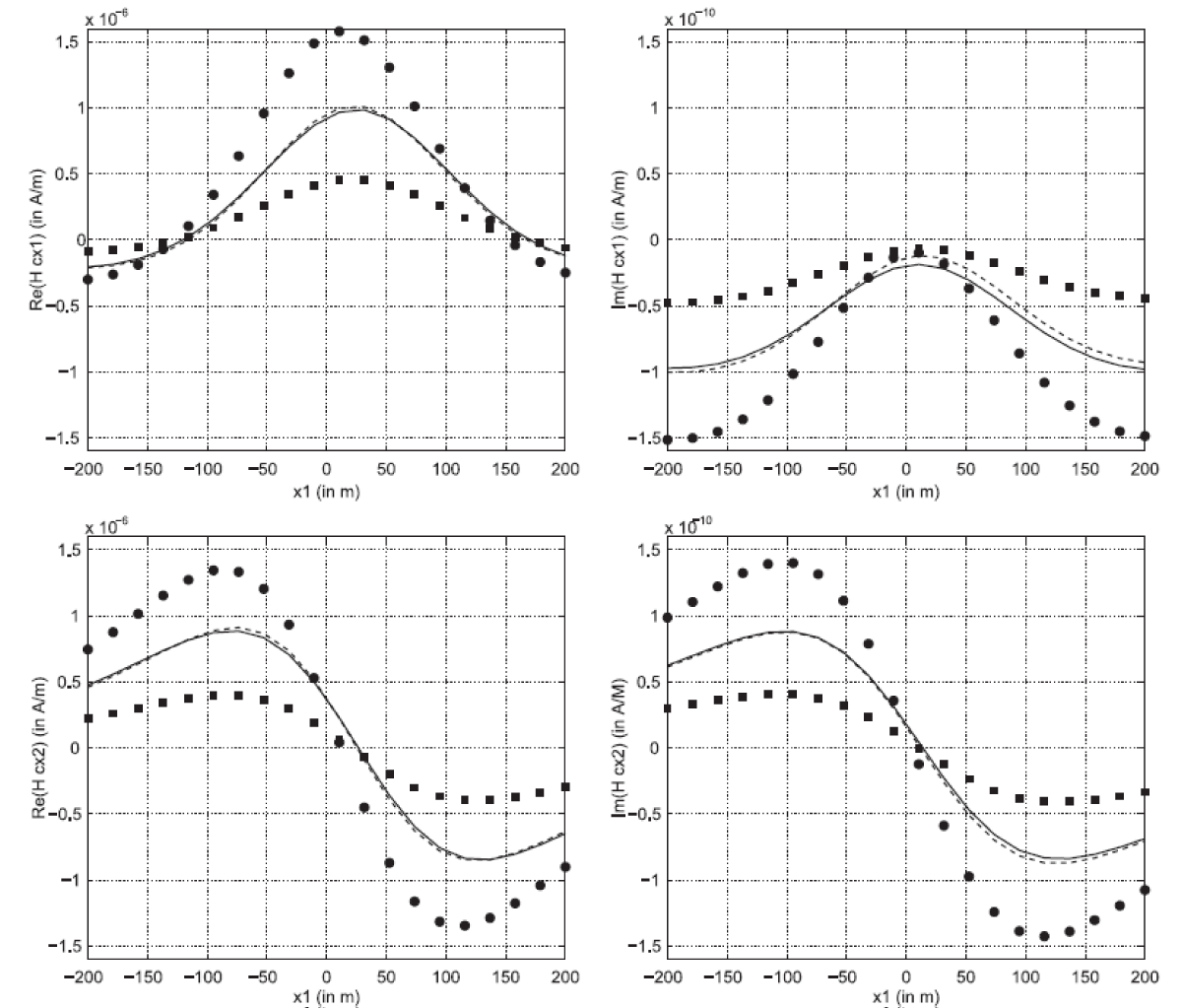Figure 3: Real (left column) and imaginary (right column) pa...
Dassios G. Ellipsoidal harmonics: theory and applications. Cambridge: Cambridge University Press; 2012.
Moon P, Spencer E. Field theory handbook. Berlin: Springer-Verlag; 1971.
Morse PM, Feshbach H. Methods of theoretical physics. Vols. I & II. New York: McGraw-Hill; 1953.
Hobson EW. The theory of spherical and ellipsoidal harmonics. New York: Chelsea Publishing Company; 1965.
Dassios G, Satrazemi K. Lamé functions and ellipsoidal harmonics up to degree seven. Int J Spec Funct Appl. 2014;2(1):27-40.
Dassios G, Kariotou F, Vafeas P. Invariant vector harmonics: the ellipsoidal case. J Math Anal Appl. 2013;405:652-60.
Fragoyiannis G, Vafeas P, Dassios G. On the reducibility of the ellipsoidal system. Math Methods Appl Sci. 2022;45:4497-4554.
Kariotou F. On the mathematics of EEG and MEG in spheroidal geometry. Bull Greek Math Soc. 2003;47:117-35.
Dassios G, Fokas AS, Hadjiloizi D. On the complementarity of electroencephalography and magnetoencephalography. Inverse Problems. 2007;23:2541.
Dassios G, Doschoris M, Satrazemi K. Localizing brain activity from multiple distinct sources via EEG. J Appl Math. 2014;2014:232747.
Dassios G, Hadjiloizi D. On the non-uniqueness of the inverse problem associated with electroencephalography. Inverse Problems. 2009;25:115012.
Dassios G, Fragoyiannis G, Satrazemi K. On the inverse EEG problem for a 1D current distribution. J Appl Math. 2014;2014:715785.
Dassios G, Satrazemi K. Inversion of electroencephalography data for a 2D current distribution. Math Methods Appl Sci. 2014;38:1098-1105.
Dassios G, Doschoris M, Satrazemi K. On the resolution of synchronous dipolar excitations via MEG measurements. Q Appl Math. 2018;76:39-45.
Doschoris M, Dassios G, Fragoyiannis G. Sensitivity analysis of the forward electroencephalographic problem depending on head shape variations. Math Probl Eng. 2015;2015:1-14.
Doschoris M, Vafeas P, Fragoyiannis G. The influence of surface deformations on the forward magnetoencephalographic problem. SIAM J Appl Math. 2018;78:963-76.
Papargiri A, Kalantonis VS, Vafeas P, Doschoris M, Kariotou F, Fragoyiannis G. On the geometrical perturbation of a three-shell spherical model in electroencephalography. Math Methods Appl Sci. 2022;45:8876-89.
Papargiri A, Kalantonis VS, Fragoyiannis G. Mathematical modeling of brain swelling in electroencephalography and magnetoencephalography. Mathematics. 2023;11:2582.
Dassios G, Vafeas P. Connection formulae for differential representations in Stokes flow. J Comput Appl Math. 2001;133:283-94.
Dassios G, Vafeas P. The 3D Happel model for complete isotropic Stokes flow. Int J Math Math Sci. 2004;46:2429-41.
Dassios G, Vafeas P. On the spheroidal semiseparation for Stokes flow. Res Lett Phys. 2008;2008:135289:1-4.
Vafeas P, Protopapas E, Hadjinicolaou M. On the analytical solution of the Kuwabara-type particle-in-cell model for the non-axisymmetric spheroidal Stokes flow via the Papkovich - Neuber representation. Symmetry. 2022;14:170:1-21.
Svarnas P, Papadopoulos PK, Vafeas P, Gkelios A, Clément F, Mavon A. Influence of atmospheric pressure guided streamers (plasma bullets) on the working gas pattern in air. IEEE Trans Plasma Sci. 2014;42:2430-1.
Vafeas P, Bakalis P, Papadopoulos PK. Effect of the magnetic field on the ferrofluid flow in a curved cylindrical annular duct. Phys Fluids. 2019;31:117105:1-15.
Vafeas P, Perrusson G, Lesselier D. Low-frequency solution for a perfectly conducting sphere in a conductive medium with dipolar excitation. Prog Electromagn Res. 2004;49:87-111.
Stefanidou E, Vafeas P, Kariotou F. An analytical method of electromagnetic wave scattering by a highly conductive sphere in a lossless medium with low-frequency dipolar excitation. Mathematics. 2021;9:3290:1-25.
Vafeas P, Papadopoulos PK, Lesselier D. Electromagnetic low-frequency dipolar excitation of two metal spheres in a conductive medium. J Appl Math. 2012;628261:1-37.
Vafeas P, Lesselier D, Kariotou F. Estimates for the low-frequency electromagnetic fields scattered by two adjacent metal spheres in a lossless medium. Math Methods Appl Sci. 2015;38:4210-37.
Vafeas P, Perrusson G, Lesselier D. Low-frequency scattering from perfectly conducting spheroidal bodies in a conductive medium with magnetic dipole excitation. Int J Eng Sci. 2009;47:372-90.
Vafeas P. Dipolar excitation of a perfectly electrically conducting spheroid in a lossless medium at the low-frequency regime. Adv Math Phys. 2018;9587972:1-20.
Vafeas P, Papadopoulos PK, Ding P-P, Lesselier D. Mathematical and numerical analysis of low-frequency scattering from a PEC ring torus in a conductive medium. Appl Math Model. 2016;40:6477-500.
Vafeas P. Low-frequency electromagnetic scattering by a metal torus in a lossless medium with magnetic dipolar illumination. Math Methods Appl Sci. 2016;39:4268-92.
Stratton JA. Electromagnetic theory. New York: McGraw-Hill; 1941.
Maxwell JC. A treatise on electricity and magnetism. Vols. I & II. Oxford: Oxford University Press; 1998.
Dassios G, Fokas AS. Electroencephalography and magnetoencephalography. Boston: De Gruyter; 2020.
Dassios G, Fokas AS. The definite non-uniqueness results for deterministic EEG and MEG data. Inverse Problems. 2013;29:065012.
Dassios G. Electric and magnetic activity of the brain in spherical and ellipsoidal geometry. In: Ammari H, editor. Mathematical modeling in biomedical imaging I. Berlin: Springer. 2009; 133-202.
Fokas AS. Electro-magneto-encephalography for a three-shell model: distributed current in arbitrary, spherical and ellipsoidal geometries. J R Soc Interface. 2009 May 6;6(34):479-88. doi: 10.1098/rsif.2008.0309. Epub 2008 Aug 29. PMID: 18757270; PMCID: PMC2659695.
Dassios G, Fokas AS. Electro-magneto-encephalography for a three-shell model: dipoles and beyond for the spherical geometry. Inverse Problems. 2009;25:035001.
Kariotou F. Electroencephalography in ellipsoidal geometry. J Math Anal Appl. 2004;290:324-42.
Giapalaki S, Kariotou F. The complete ellipsoidal shell model in EEG imaging. Abstr Appl Anal. 2006;2006:57429.
Doschoris M, Kariotou F. Quantifying errors during the source localization process in electroencephalography for confocal systems. IMA J Appl Math. 2018;83:243-60.
Doschoris M, Kariotou F. Error analysis for nonconfocal ellipsoidal systems in the forward problem of electroencephalography. Math Methods Appl Sci. 2018;41:6793-813.
Dassios G, Kariotou F. Magnetoencephalography in ellipsoidal geometry. J Math Phys. 2003;44:220-41.
Dassios G, Giapalaki SN, Kandili AN, Kariotou F. The exterior magnetic field for the multilayer ellipsoidal model of the brain. Q J Mech Appl Math. 2007;60:1-25.
Dassios G, Hadjiloizi D, Kariotou F. The octapolic ellipsoidal term in magnetoencephalography. J Math Phys. 2009;50:013508.
Vafeas P, Dassios G. Stokes flow in ellipsoidal geometry. J Math Phys. 2006;47:093102:1-38.
Hatzikonstantinou PM, Vafeas P. A general theoretical model for the magnetohydrodynamic flow of micropolar magnetic fluids: application to Stokes flow. Math Methods Appl Sci. 2010;33:233-48.
Stratton JA. Electromagnetic theory. New York: McGraw-Hill; 1941.
Ammari H, Kang H. Polarization and moment tensors: with applications to inverse problems and effective medium theory. Applied Mathematical Sciences. Vol. 162. New York: Springer-Verlag; 2007.
Björkberg J, Kristenson G. Three-dimensional subterranean target identification by use of optimization techniques. Prog Electromagn Res. 1997;15:141-64.
Yu T, Carin L. Analysis of the electromagnetic inductive response of a void in a conducting-soil background. IEEE Trans Geosci Remote Sens. 2000;38:1320-7.
Huang H, Won IJ. Detecting metal objects in magnetic environments using a broadband electromagnetic method. Geophysics. 2003;68:1877-87.
Cui TJ, Chew WC, Wright DL, Smith DV. Three-dimensional imaging for buried objects in a very lossy earth by inversion of VETEM data. IEEE Trans Geosci Remote Sens. 2003;41:2197-210.
Tortel H. Electromagnetic imaging of a three-dimensional perfectly conducting object using a boundary integral formulation. Inverse Problems. 2004;20:385-98.
Perrusson G, Vafeas P, Lesselier D. Low-frequency dipolar excitation of a perfect ellipsoidal conductor. Q Appl Math. 2010;68:513-36.
Perrusson G, Vafeas P, Chatjigeorgiou IK, Lesselier D. Low-frequency on-site identification of a highly conductive body buried in Earth from a model ellipsoid. IMA J Appl Math. 2015;80:963-80.
Vafeas P. Low-frequency dipolar electromagnetic scattering by a solid ellipsoid in the lossless environment. Stud Appl Math. 2020;145:217-46.
