
Deep Learning-based Multi-class Three-dimensional (3-D) Object Classification using Phase-only Digital Holographic Information
Machine Learning Data EngineeringArtificial Intelligence受け取った 27 Jun 2024 受け入れられた 08 Jul 2024 オンラインで公開された 09 Jul 2024
Focusing on Biology, Medicine and Engineering ISSN: 2995-8067 | Quick Google Scholar
Next Full Text
The Power of Artificial Intelligence for Improved Patient Outcomes, Ethical Practices and Overcoming Challenges


受け取った 27 Jun 2024 受け入れられた 08 Jul 2024 オンラインで公開された 09 Jul 2024
In this paper, we present a deep CNN-based approach for multi-class classification of three-dimensional (3-D) objects using phase-only digital holographic information. The 3-D objects considered for the multi-class (four-class) classification task are ‘triangle-square’, ‘circle-square’, ‘square-triangle’, and ‘triangle-circle’. The 3-D object ‘triangle-square’ is considered for Class-1 and the remaining 3-D objects ‘circle-square’, ‘square-circle’, and ‘triangle-circle’ are considered for Class-2, Class-3, and Class-4. The digital holograms of 3-D objects were created using the two-step Phase-Shifting Digital Holography (PSDH) technique and were computationally post-processed to obtain phase-only digital holographic data. Subsequently, a deep CNN was trained on a phase-only image dataset consisting of 2880 images to produce the results. The loss and accuracy curves are presented to validate the performance of the model. Additionally, the results are validated using metrics such as the confusion matrix, classification report, Receiver Operating Characteristic (ROC) curve, and precision-recall curve.
Deep learning, a branch of artificial intelligence (AI), encompasses various deep neural networks, including Convolutional Neural Network (CNN), AlexNet, Visual Geometry Group (VGG) Networks, U-Net, Y-Net, and Convolutional Encoder-Decoder Network models. These networks have been utilized in various digital holographic applications, including focus prediction [1], depth prediction [2], image segmentation [3], hologram reconstruction [4], 3-D object binary classification [5], 3-D object binary regression [6,7], 3-D object multi-class classification and multi-output regression [8-10], and phase unwrapping [11]. Digital holography is an optical imaging technique that records 3-D information about an object using an electronic sensor such as a Charge-Coupled Device (CCD) or Complementary Metal Oxide Semiconductor (CMOS) sensor. The hologram recorded using a CCD sensor is numerically reconstructed to obtain a complex-valued image containing both intensity and phase information. This phase (depth) information can be utilized for AI-based supervised learning techniques such as classification and regression tasks. Classification is a supervised learning technique that defines the decision boundary between the input data and the target labels. The classification technique produces output as discrete labels. In this study, multi-class (four-class) classification of 3-D objects was performed using a deep CNN. A CNN is a deep neural network that consists of distinct layers for feature extraction and classification. The feature extraction component includes multiple convolutional and pooling layers. The convolutional layer performs a convolution operation between the input and the kernel to produce a feature map. This feature map is then processed through the pooling layer to reduce its dimensionality. The classification component comprises fully connected layers and an output layer to generate the final results. Zifei Li, et al. [12] introduced a deep CNN for binary classification of speckle patterns acquired from multi-mode fiber. Priscoli, et al. [13] explored both machine learning and deep learning techniques, including Principal Component Analysis (PCA), Multi-Layer Perceptron (MLP), and CNN, for binary classification of cancer cells in microfluidics. Additionally, Lam, et al. [14] proposed a deep CNN for hologram classification of occluded and deformable objects, addressing holograms contaminated with speckle noise. Cheng, et al. [15] introduced a deep CNN tailored for pattern classification of digital holographic data. Zhang, et al. [16] developed a deep CNN specifically for classifying marine plankton from digital holograms. Zhu, et al. [17] proposed an automated method for classifying microplastics in digital holographic data using deep learning and generative adversarial networks. The current study presents a multi-class (four-class) classification of 3-D objects, specifically ‘triangle-square’, ‘circle-square’, ‘square-triangle’, and ‘triangle-circle’, utilizing phase-only digital holographic information acquired from the Phase-Shifting Digital Holography (PSDH) technique through deep CNN. The primary distinction between this work and prior studies [12-17] lies in the utilization of deep CNN for multi-class (four-class) classification of 3-D objects based on phase-only digital holographic data acquired via phase-shifting digital holography. The results of the classification task are delineated in terms of loss and accuracy curves to validate the proof of concept. Furthermore, the work is validated with results including the confusion matrix, classification report, Receiver Operating Characteristic (ROC) curve, and precision-recall curve. Classifying phase images entails the classification of 3-D objects using deep CNN. The major contribution of this paper is this is the first work reported to perform a four-class classification of 3-D objects using phase-shifting digital holographic data.
Figure 1 depicts a block diagram illustrating the CNN architecture employed for multi-class (four-class) classification of 3-D objects utilizing a phase-only image dataset. The CNN takes the input as the phase-only image of size 512 × 512 from the digital hologram. The CNN depicted in Figure 1 comprises four convolutional and four pooling layers in the feature extraction stage, followed by fully connected and output layers in the classification stage. In the convolutional layer, the input phase image undergoes convolution with a kernel to generate the feature map. The output of the convolutional layer is determined by
(1)
In the above eqn. (1), represents the output feature map and Xpq represents the input phase image. represents kernel coefficients, k represents the number of kernels, t represents the kernel size, P represents the activation function, and Bpq represents bias. The number of kernels in the convolutional layer is k = 8,16,32,64. The size of the kernel is t = 5 × 5. The activation function P represents the rectified linear unit (ReLU) activation function that is present in convolutional and fully connected layers. The output of the convolutional layer is then fed into the pooling layer, where the Max-Pooling2D technique is applied to further decrease the dimensionality of the feature map. The output of the pooling layer is determined by
Ypq = Xpq (2)
In the above eqn. (2), Ypq represents the output feature map and Xpq represents the input. The output of the final pooling layer is flattened and subsequently passed to the fully connected layer. The output of the fully connected layer is determined by
(3)
In the above eqn. (3), Yp represents the output of the fully connected layer, Bp represents the bias, P represents the ReLU activation function, Wmn represents weight values, Xp represents the one-dimensional (1-D) data obtained through the flattening layer, and t represents the number of neurons. The output of the final pooling layer is 28 × 28 × 64. The number of neurons selected in the fully connected layer is t = 64. The output of the fully connected layer is forwarded to the output layer. In the output layer, a subset of four neurons is selected from the sixty-four neurons, utilizing the softmax activation function to generate the final output. The equation for the softmax activation function is expressed as
(4)
In the above eqn. (4), Qk represents the output, Mk represents the input, and t represents several neurons.
For the four-class classification task, the following four 3-D objects were included: ‘triangle-square’, ‘circle-square’, ‘square-triangle’, and ‘triangle-circle’. These objects were distributed among four distinct subclasses: Class-1, Class-2, Class-3, and Class-4. Specifically, the 3-D object ‘triangle-square’ was designated as belonging to Class-1. Following the classification scheme, the subsequent 3-D object, ‘circle-square’, was assigned to Class-2. Similarly, the 3-D object ‘square-triangle’ was allocated to Class 3. Finally, the last 3-D object, ‘triangle-circle’, was designated as belonging to Class-4. The 3-D object ‘circle-square’ was structured such that the circular feature resided prominently in the first plane, while the square feature was distinctly positioned in the subsequent plane. Each plane is separated by various distances d1, and d2 respectively. The remaining three 3-D objects were constructed similarly, with the distinction that different features were allocated to the first and second planes, respectively. Two phase-shifted holograms of 00 and 900 were formed at the camera plane and these holograms were post-processed to obtain a complex-valued image containing intensity and phase information using a two-step phase-shifting digital holography (PSDH) technique. The holograms and reconstructed intensity/phase images are of size 1024 × 1024. The intensity and phase images were reconstructed at both distances. In Figure 2a, a schematic representation of the 3-D object volume ‘triangle-square’, belonging to Class-1, is depicted, illustrating the distribution of information across both the first and second planes. Additionally, Figure 2a illustrates the geometry for digital hologram recording from two-step phase-shifted plane reference waves.
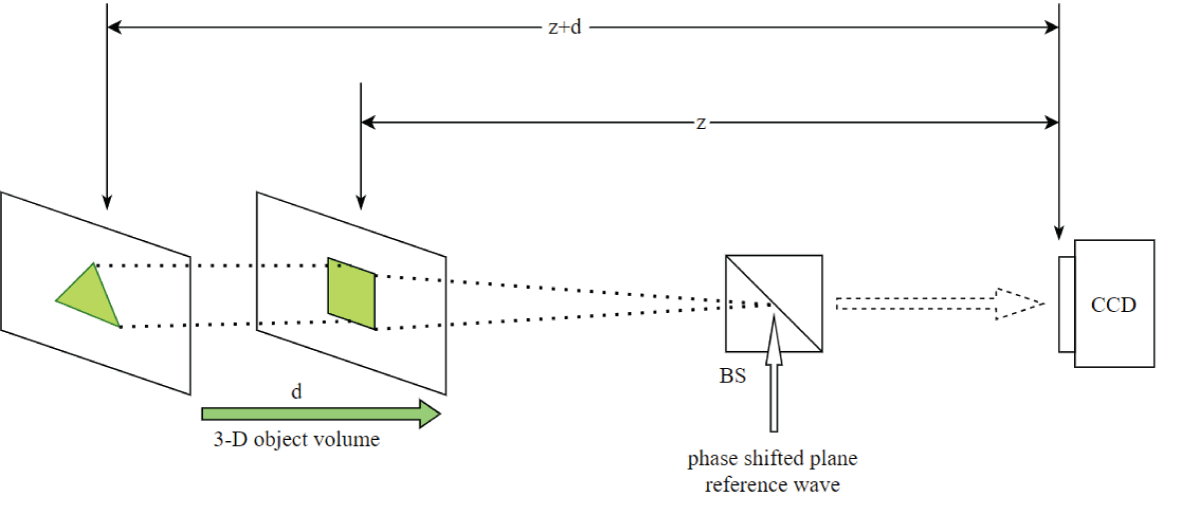 Figure 2: Schematic of the geometry for the recording of the digital hologram of 3-D object volume with different features in the first and second planes and separating distances z =10 cm and d = 2 cm. (a) triangle-square. BS: beam splitter CCD: charge-coupled device.
Figure 2: Schematic of the geometry for the recording of the digital hologram of 3-D object volume with different features in the first and second planes and separating distances z =10 cm and d = 2 cm. (a) triangle-square. BS: beam splitter CCD: charge-coupled device.The digital holograms of four different 3-D objects namely ‘triangle-square’, ‘circle-square’, ‘square-triangle’, and ‘triangle-circle’ belonging to four-different sub-classes were further rotated in steps of 0.5° separately forming a dataset of 2880 holograms. Similarly, the reconstructed intensity/phase images obtained from the two-step Phase-Shifting Digital Holography (PSDH) technique were also rotated in steps of 0.5° to form a dataset of 2880 images separately for intensity and phase information. For the multi-class classification (four-class classification) of 3-D objects, only phase information was taken into account. The dataset, comprising 2880 phase images, was divided into training, validation, and test sets, containing 2160 (75%), 432 (15%), and 288 (10%) images, respectively. for the training of the deep CNN, the size of the phase image considered was 512 × 512 from 1024 × 1024. The deep CNN was trained for 50 epochs on the phase-only image dataset using an Adam optimizer with a learning rate of 0.0007, while categorical cross-entropy was employed as the loss function. The implementation of the deep CNN was carried out in a TensorFlow environment using Python programming. Figure 3 displays samples of three reconstructed phase images corresponding to 3-D objects, namely ‘triangle-square’, ‘circle-square’, and ‘triangle-circle’, which belong to Class-1, Class-2, and Class-4, respectively.
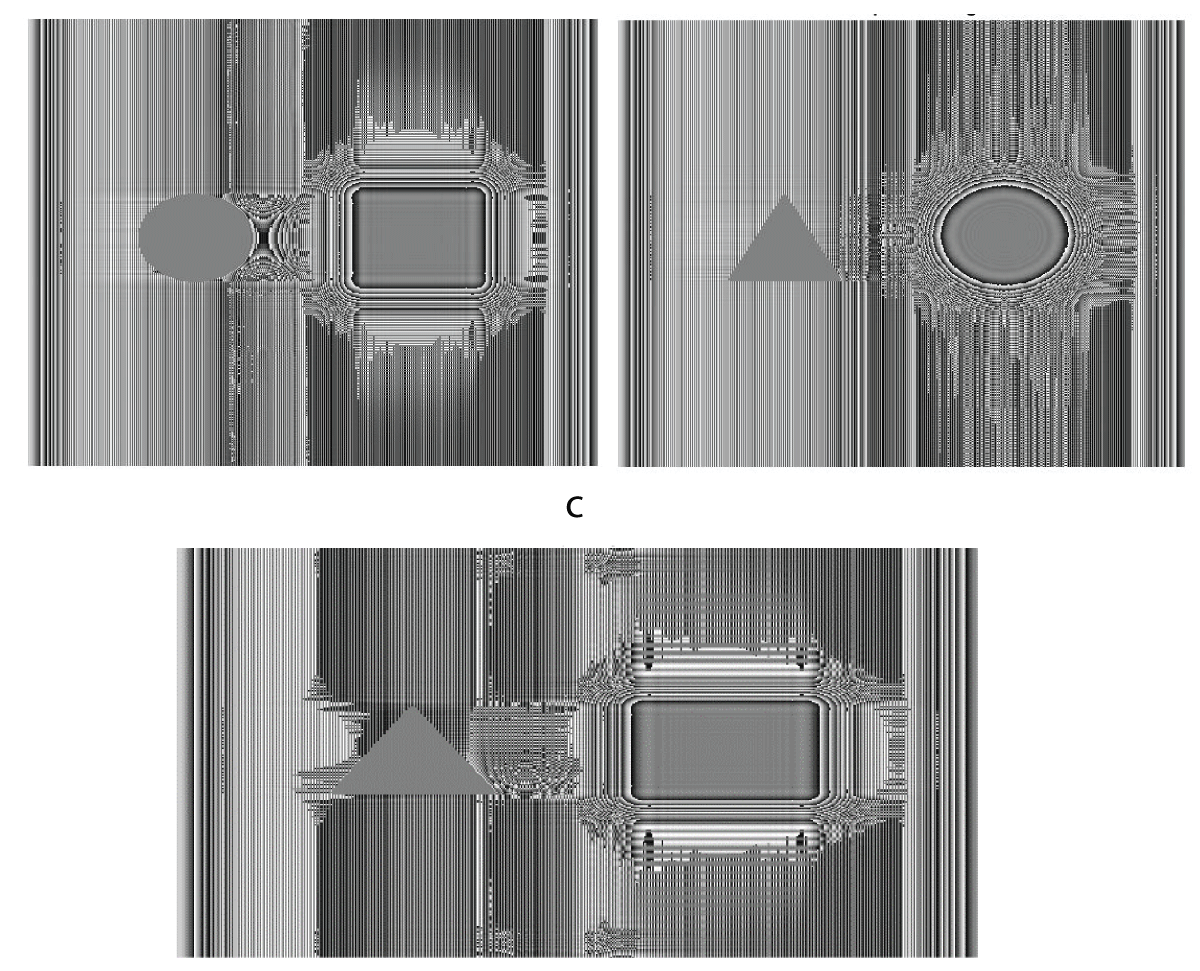 Figure 3: Reconstructed phase-only images of 3-D objects (a) circle-square (b) triangle-circle (c) triangle-square.
Figure 3: Reconstructed phase-only images of 3-D objects (a) circle-square (b) triangle-circle (c) triangle-square.The deep CNN was trained on a batch of 54 images from the training set and a batch of 24 images from the validation set of the phase-only image dataset in a single epoch. Subsequently, each epoch was iteratively iterated over 40/18 steps on the training/validation sets to complete the training process. Figure 4 illustrates the loss/accuracy curves obtained from the training/validation sets after completing the training for 50 epochs on the phase-only image dataset.
From Figure 4a, it can be said that the training loss is decreasing and the validation loss is fluctuating. After the completion of the training for fifty epochs, the training loss is 0.0015and the validation loss is 0.5771. So it can be said that the training loss is lower compared to the validation loss. Next from Figure 4b, it can be said that the training accuracy is increasing initially and then becomes constant. i.e. training accuracy increases initially till around ten epochs and then becomes constant around 1.00 after 10 epochs and remains at a value of 1.00 till 50 epochs. The validation accuracy increases in the beginning till around 10 epochs and then starts fluctuating around 0.80 after 10 epochs. So it can be observed that from Figure 4b, the training accuracy is greater than the validation accuracy i.e. the margin between the training accuracy and validation accuracy is more. So it can be said that the deep CNN model is Overfitting on the phase-only image dataset for the four-class classification task. The deep CNN model was tested using 24 phase-only images from the test set. Furthermore, the performance of the four-class classification task is illustrated by a multi-class confusion matrix. This matrix shows the number of images correctly and incorrectly classified for each class. Figure 5 presents the confusion matrix for the four classes, as obtained from the Deep CNN model on the phase-only image dataset. The multi-class classification task can be done for any number of classes. Here, four classes have been considered for the multi-class classification task. In general, n classes can be considered to perform multi-class classification tasks.
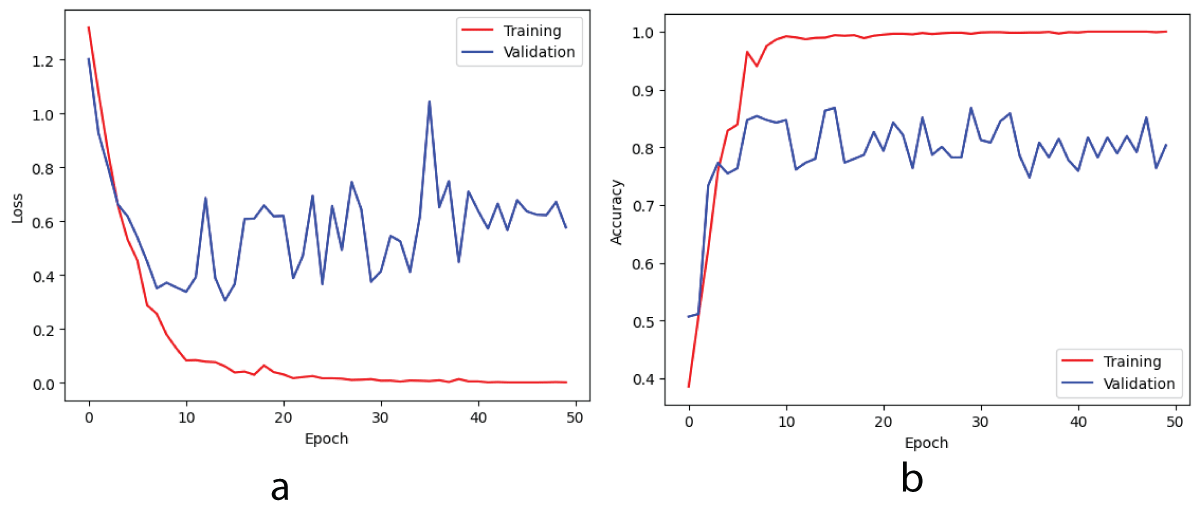 Figure 4: Loss and accuracy curves on training/validation sets for phase-only image dataset (a) loss (b) accuracy.
Figure 4: Loss and accuracy curves on training/validation sets for phase-only image dataset (a) loss (b) accuracy.From Figure 5, it can be observed that the confusion matrix is represented for the four classes on the phase-only image dataset obtained from the deep CNN model. For Class-1, 22 images are predicted as FALSE and 2 as TRUE. For Class-2, 16 images are predicted as FALSE and 8 as TRUE. For Class-3, 17 images are predicted as FALSE and 7 as TRUE. Finally, for Class-4, 17 images are predicted as FALSE and 7 as TRUE. For Class 1, 22 images are recognized as true positive (TP), 2 images are recognized as true negative (TN), and finally 0 images are recognized as false positive (FP) and false negative (FN) respectively. For Class 2, 11 images are recognized as true negative (TN), 8 images as true positive (TP), 5 images as false positive (FP), and 0 images as false negative (FN) respectively. For Class 3, 17 images are recognized as true negative (TN), 3 images are recognized as true positive (TP), 4 images are recognized as false negative (FN), and 0 images as false positive (FP) respectively. For Class 4, 17 images are recognized as true negative (TN), 6 images are recognized as true positive (TP), 1 image as false negative (FN), and 0 images as false positive (FP) respectively. The performance metrics namely accuracy, positive predictive value (PPV), sensitivity, and F1-Score are calculated for all four classes namely Class 1, Class 2, Class 3, and Class 4 for both TRUE and FALSE classes. The metric accuracy is calculated by taking the ratio of the sum of true positives and true negatives to the sum of true positives, true negatives, false negatives, and false positives respectively. The metric positive predictive value is calculated by taking the ratio of true positives to the sum of true positives and false positives respectively. The metric sensitivity is calculated by taking the ratio of true positives to the sum of true positives and false negatives respectively. The metric F1-score is calculated by taking the ratio of the sum of twice of true positives to the sum of twice of true positives, false positives, and false negatives respectively. The metric mean squared error is calculated by taking the squared difference between ground truth and predicted values. The metric mean absolute error is calculated by taking the difference between the ground truth and the predicted values. The classification report from the deep CNN model for all four classes on the phase-only image dataset is shown in Table 1.
| Table 1: Classification Report obtained from Deep CNN model on phase-only image dataset. | |||||||
| Label | Positive Predictive Value (PPV) | Sensitivity | F1-Score | Support | Mean Square Error (MSE) | Mean Absolute Error (MAE) | Class 1 |
| Not 1 (FALSE class) | 1.00 | 1.00 | 1.00 | 22 | |||
| 1 (TRUE class) | 1.00 | 1.00 | 1.00 | 2 | 0.12 | 0.12 | |
| Accuracy | 1.00 | 24 | |||||
| Macro average | 1.00 | 1.00 | 1.00 | 24 | |||
| Weighted average | 1.00 | 1.00 | 1.00 | 24 | |||
| Label | Positive Predictive Value (PPV) | Sensitivity | F1-Score | Support | Mean Square Error (MSE) | Mean Absolute Error (MAE) | Class 2 |
| Not 1 (FALSE class) | 1.00 | 0.69 | 0.81 | 16 | |||
| 1 (TRUE class) | 0.62 | 1.00 | 0.76 | 8 | 0.12 | 0.12 | |
| Accuracy | 0.79 | 24 | |||||
| Macro average | 0.81 | 0.84 | 0.79 | 24 | |||
| Weighted average | 0.87 | 0.79 | 0.80 | 24 | |||
| Label | Positive Predictive Value (PPV) | Sensitivity | F1-Score | Support | Mean Square Error (MSE) | Mean Absolute Error (MAE) | Class 3 |
| Not 1 (FALSE class) | 0.81 | 1.00 | 0.89 | 17 | |||
| 1 (TRUE class) | 1.00 | 0.43 | 0.60 | 7 | 0.33 | 0.33 | |
| Accuracy | 0.83 | 24 | |||||
| Macro average | 0.90 | 0.71 | 0.75 | 24 | |||
| Weighted average | 0.87 | 0.83 | 0.81 | 24 | |||
| Label | Positive Predictive Value (PPV) | Sensitivity | F1-Score | Support | Mean Square Error (MSE) | Mean Absolute Error (MAE) | Class 4 |
| Not 1 (FALSE class) | 0.94 | 1.00 | 0.97 | 17 | |||
| 1 (TRUE class) | 1.00 | 0.86 | 0.92 | 7 | 0.42 | 0.42 | |
| Accuracy | 0.96 | 24 | |||||
| Macro average | 0.97 | 0.93 | 0.95 | 24 | |||
| Weighted average | 0.96 | 0.96 | 0.96 | 24 | |||
Table 1 highlights that the deep CNN model achieves higher accuracy for Class 1 compared to the other classes, with perfect (unity) values for Positive Predictive Value (PPV), sensitivity, and F1-score in both the FALSE and TRUE classes. The macro average is computed by averaging these metrics across TRUE and FALSE classes, while the weighted average combines macro and micro averages. For Class 1, the deep CNN model achieves unity values for both macro and weighted averages. In Class 2, the model demonstrates higher sensitivity but lower PPV for the TRUE class, and conversely, lower sensitivity and higher PPV for the FALSE class. The macro average results in the value of 0.81 for positive predictive value (PPV), 0.84 for sensitivity, and 0.79 for F1-score labels respectively. The weighted average results in the value of 0.87 for PPV, 0.79 for sensitivity, and 0.80 for F1-score labels respectively. The metrics mean squared error (MSE) and Mean Absolute Error (MAE) for the TRUE class are 0.12, and 0.12 for Classes 1 and 2 respectively. The deep CNN model has Classes 3 and 4 exhibits a pattern where PPV is higher but sensitivity is lower for the TRUE class compared to the FALSE class. In Class 3, the macro average results in the value of 0.90 for positive predictive value (PPV), 0.71 for sensitivity, and 0.75 for F1-score labels. The metric weighted average results in the value of 0.87 for PPV, 0.83 for sensitivity, and 0.81 for F1-score labels respectively. The mean square error (MSE) and Mean Absolute Error (MAE) values are 0.33, and 0.33 for Class 3 in the TRUE Class. In Class 4, the macro average results in the value of 0.97 for positive predictive value (PPV), 0.93 for sensitivity, and 0.95 for F1-score labels. The weighted average results in equal values for PPV, sensitivity, and F1-score labels respectively. i.e. 0.96 for PPV, sensitivity, and F1-score. The mean squared error and mean absolute error results in the values of 0.42, and 0.42 for Class 4 in the TRUE Class. Furthermore, the performance of the multi-class classification task is depicted using Receiver Operating Characteristic (ROC) curves and PPV-sensitivity characteristic curves in Figure 6. These curves illustrate how well the deep CNN model distinguishes between TRUE and FALSE classes, assessed by the area under the curve (AUC) metric.
From Figure 6, it is evident that the deep CNN model has a higher AUC value for Class 1 compared to the other classes. Figure 7 displays the Positive Predictive Value (PPV) – sensitivity characteristic curve for all four classes obtained from the deep CNN model on the phase-only image dataset.
From Figure 7, it can be observed that the deep CNN model has higher sensitivity and lower positive predictive value for Class 4. Class 1 exhibits perfect positive predictive value and sensitivity on the phase-only image dataset from the deep CNN model. Classes 2 and 3 exhibit lower Positive Predictive Value (PPV) and higher sensitivity as depicted in Figure 7.
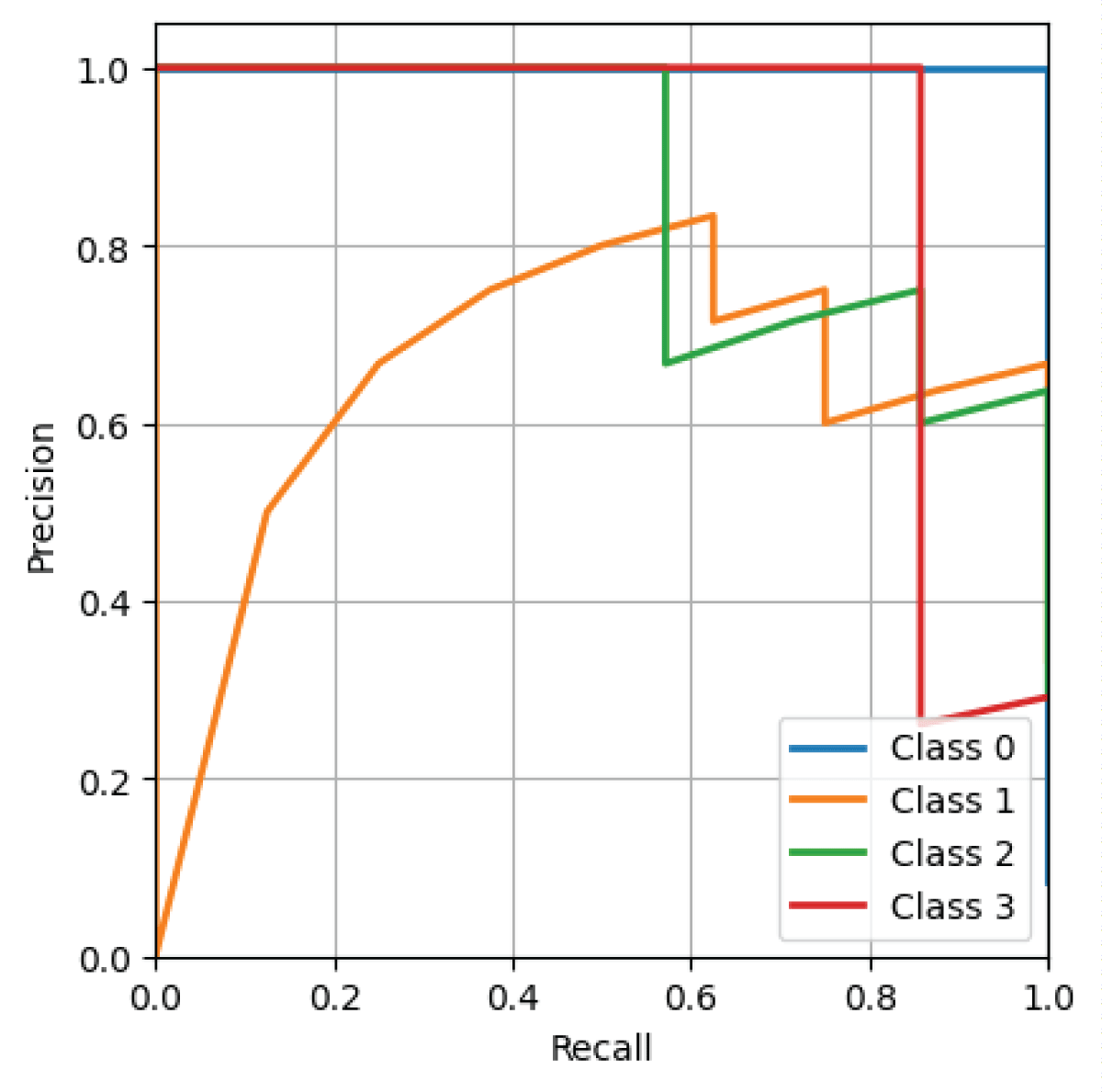 Figure 7: Positive predictive value – sensitivity characteristic obtained from deep CNN model on phase-only image dataset.
Figure 7: Positive predictive value – sensitivity characteristic obtained from deep CNN model on phase-only image dataset.RN UM, Basavaraju L. Deep Learning-based Multi-class Three-dimensional (3-D) Object Classification using Phase-only Digital Holographic Information. IgMin Res. Jul 09, 2024; 2(7): 550-557. IgMin ID: igmin216; DOI:10.61927/igmin216; Available at: igmin.link/p216
次のリンクを共有した人は、このコンテンツを読むことができます:
1Associate Professor, Dept of CSE (AI and ML), ATME College of Engineering, Mysore-570028, India
2Professor, Dept of ECE, ATME College of Engineering, Mysore-570028, India
Address Correspondence:
Uma Mahesh RN, Associate Professor, Dept of CSE (AI and ML), ATME College of Engineering, Mysore-570028, India, Email: [email protected]
How to cite this article:
RN UM, Basavaraju L. Deep Learning-based Multi-class Three-dimensional (3-D) Object Classification using Phase-only Digital Holographic Information. IgMin Res. Jul 09, 2024; 2(7): 550-557. IgMin ID: igmin216; DOI:10.61927/igmin216; Available at: igmin.link/p216
Copyright: © 2024 Uma Mahesh RN, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
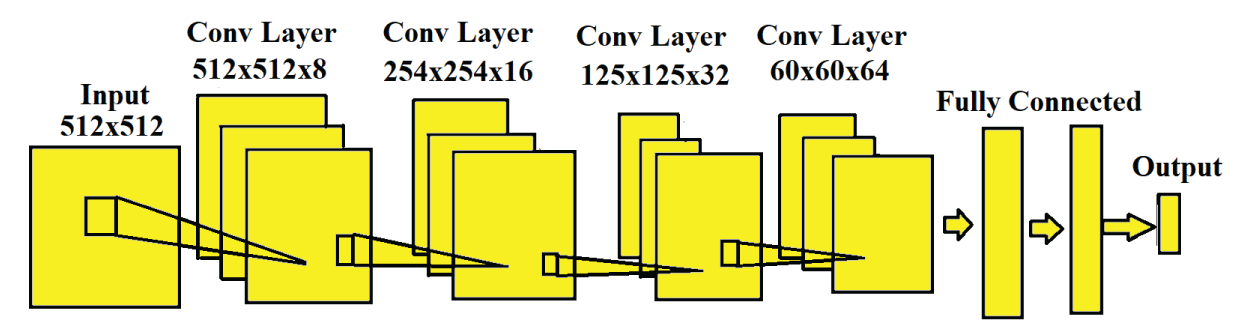 Figure 1: Block diagram of Convolutional Neural Network (CNN...
Figure 1: Block diagram of Convolutional Neural Network (CNN...
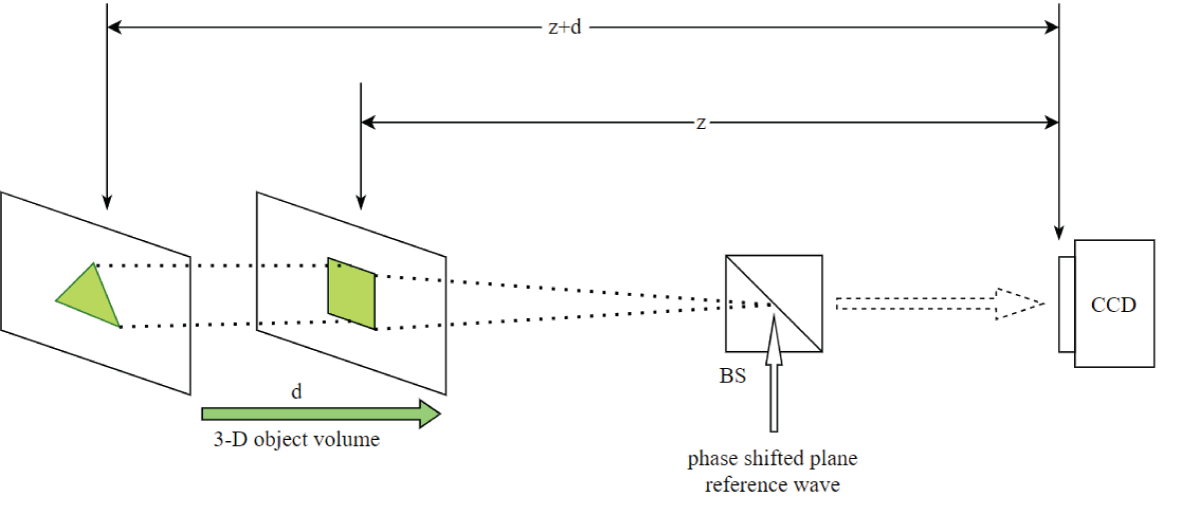 Figure 2: Schematic of the geometry for the recording of the...
Figure 2: Schematic of the geometry for the recording of the...
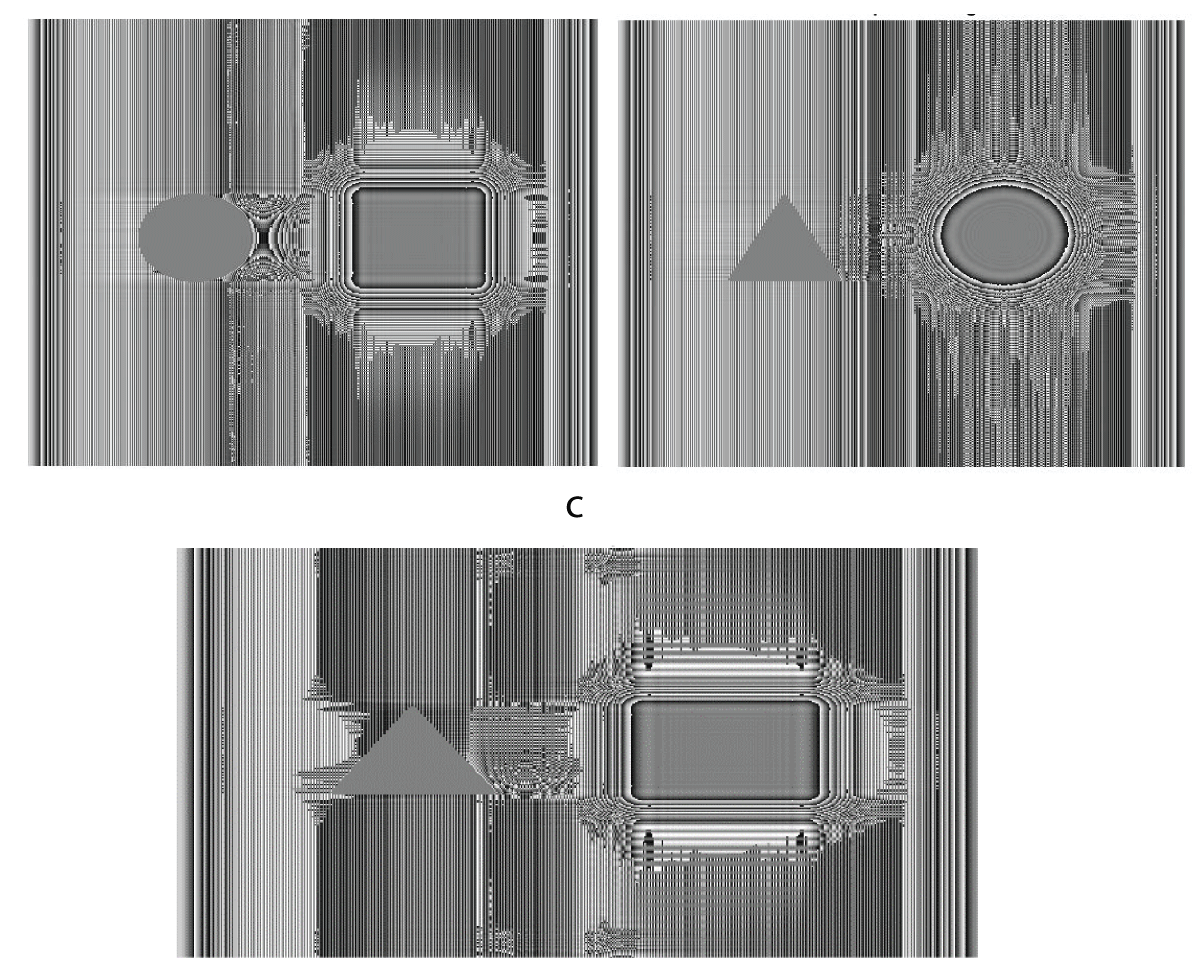 Figure 3: Reconstructed phase-only images of 3-D objects (a)...
Figure 3: Reconstructed phase-only images of 3-D objects (a)...
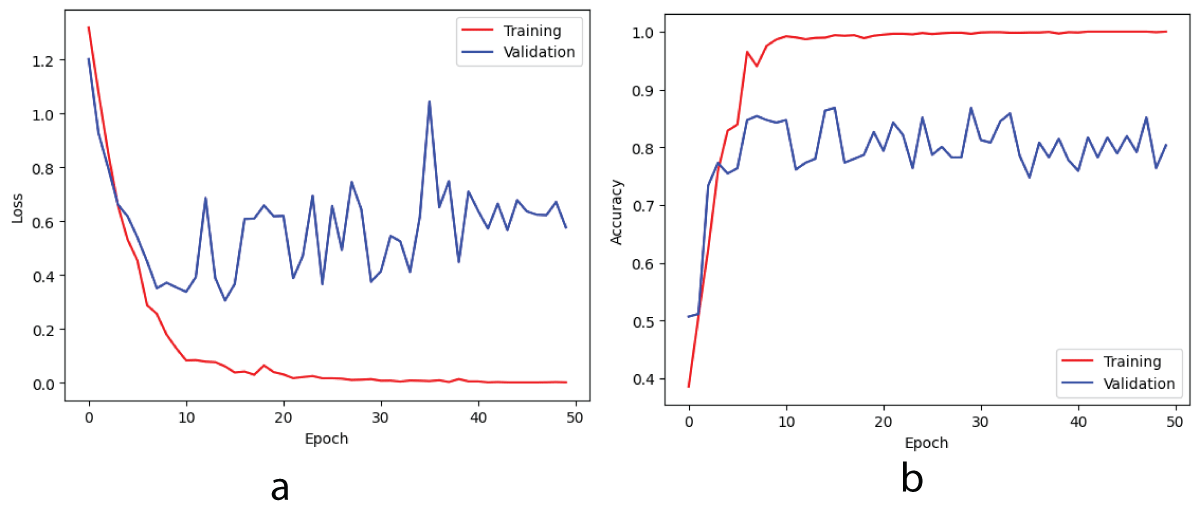 Figure 4: Loss and accuracy curves on training/validation se...
Figure 4: Loss and accuracy curves on training/validation se...
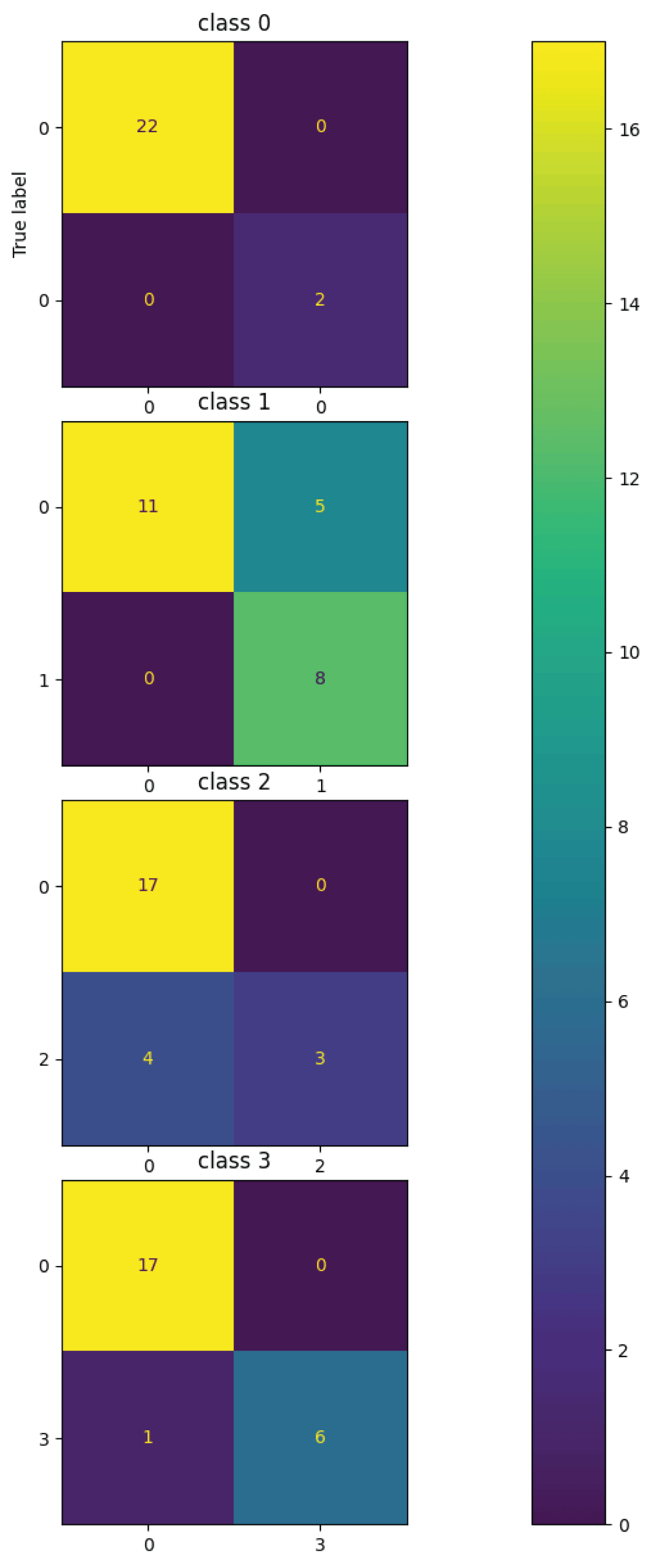 Figure 5: Multi-Class Confusion Matrix on Phase-only image d...
Figure 5: Multi-Class Confusion Matrix on Phase-only image d...
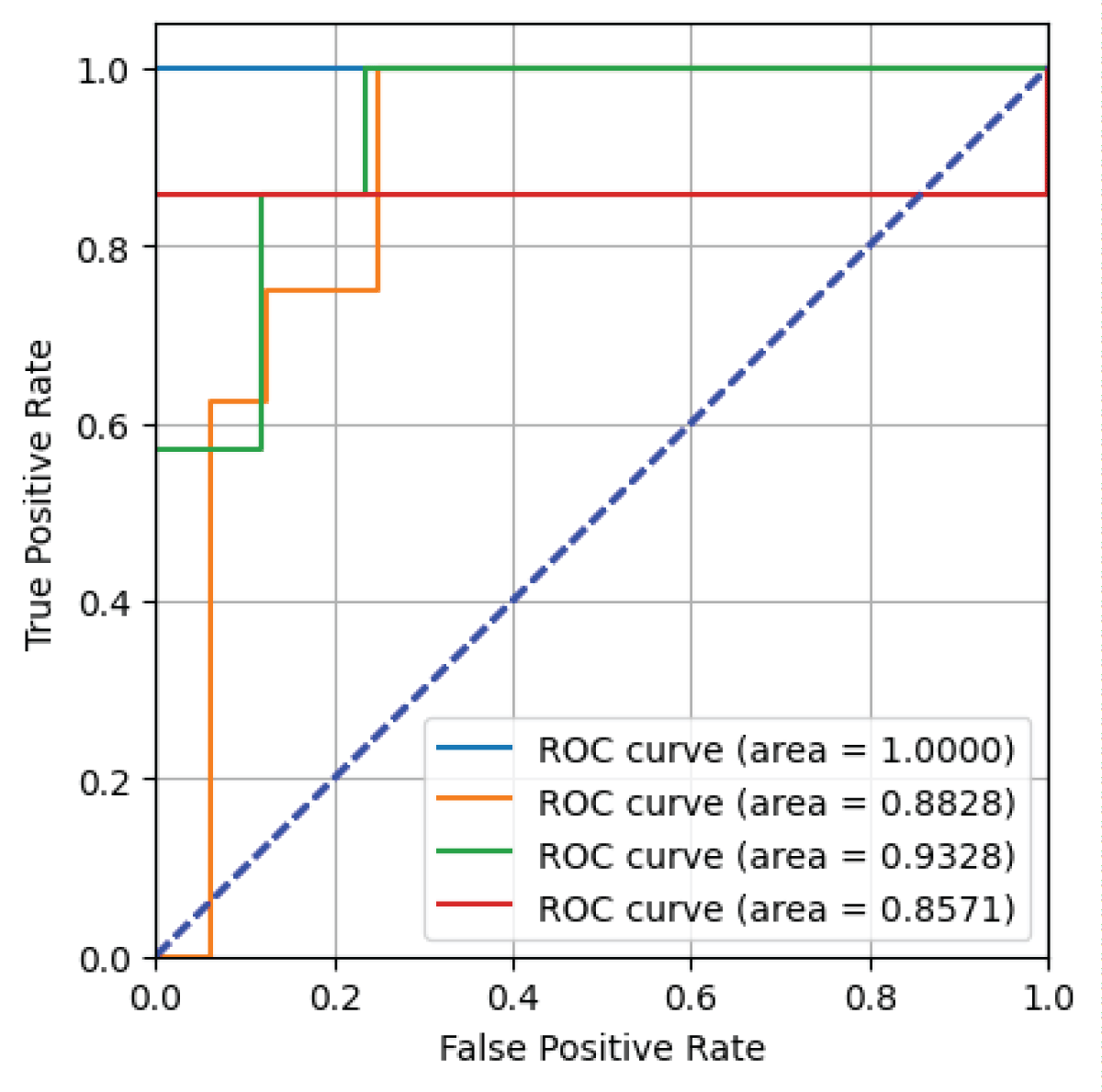 Figure 6: ROC curve obtained from deep CNN model on phase-on...
Figure 6: ROC curve obtained from deep CNN model on phase-on...
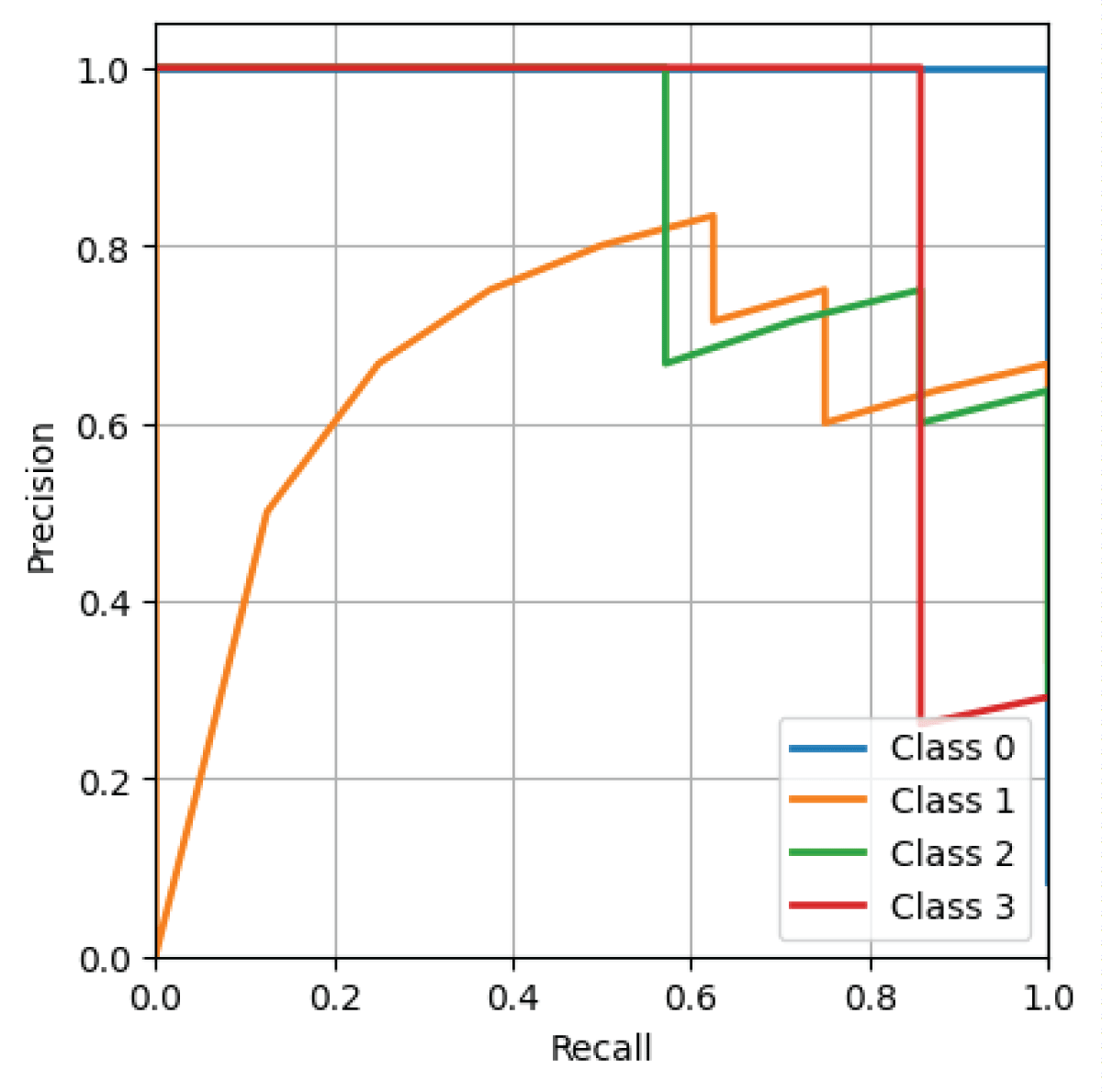 Figure 7: Positive predictive value – sensitivity characte...
Figure 7: Positive predictive value – sensitivity characte...