
Exploring Markov Decision Processes: A Comprehensive Survey of Optimization Applications and Techniques
Machine Learning Robotics受け取った 24 Jun 2024 受け入れられた 03 Jul 2024 オンラインで公開された 04 Jul 2024
ISSN: 2995-8067 | Quick Google Scholar


受け取った 24 Jun 2024 受け入れられた 03 Jul 2024 オンラインで公開された 04 Jul 2024
Markov decision process is a dynamic programming algorithm that can be used to solve an optimization problem. It was used in applications like robotics, radar tracking, medical treatments, and decision-making. In the existing literature, the researcher only targets a few applications area of MDP. However, this work surveyed the Markov decision process’s application in various regions for solving optimization problems. In a survey, we compared optimization techniques based on MDP. We performed a comparative analysis of past work of other researchers in the last few years based on a few parameters. These parameters are focused on the proposed problem, the proposed methodology for solving an optimization problem, and the results and outcomes of the optimization technique in solving a specific problem. Reinforcement learning is an emerging machine learning domain based on the Markov decision process. In this work, we conclude that the MDP-based approach is most widely used when deciding on the current state in some environments to move to the next state.
Markov Decision Process is a computational model used for dynamic programming that guides decision-making in various use areas, such as stock control, scheduling, economics, and healthcare [1]. Al-Sheikh, et al. summarized the MDP usefulness in wireless networks. His analysis examines many uses of Markov Decision Process. In addition, various modulation techniques are compared and discussed to help use MDPs in Sensor Networks [2]. A variety of medical decision-making problems have been identified in MDPs. To improve cancer detection in the long term, Petousis, et al. portrayed an imaging screening method for repeated decision-making problems and made an MDP model. Although MDPs have still not been commonly applied to the medical field, such recent significant developments have shown that MDPs can be responsible for useful clinical tools [3]. The existing studies only focus on a few application areas of MDP. Still, this study overviews the many application areas of an MDP and discusses the results and strength of existing methods.
As in the MDP model, four states (S) and three control acts (A) describe the security:
The goal is to find the defender’s optimal procedure in which the defender wants to see what action needs to be taken in every single state to maximize rewards [4].
The collaboration between an attacker and defender is differentiated equally by finite action. And states. Four tuple Markov Decision Processes (S, A, P, R) are represented by [5]:
S is a set of a finite number of states.
A is a finite number of actions to control.
P is the probability of one state to a new state.
R is estimated to receive rewards after the state changes immediately.
Decision epochs: There are five essential components for all MDP models.
First, the decision-maker must decide how much a decision is made or if such choices are taken at predefined times or different intervals. The time a decision is made is called the decision epoch [6].
State spaces and states: Second, the decision maker must determine what relevant data needs to be tracked to make an informed decision.
At decision-epoch t, the current values of the relevant information are called the state (usually represented by st) and form the basis on which decisions are taken. The state space, S, is the set of all the system’s possible states [7]. Only the state must contain relevant information that changes from decision epoch to decision epoch. Directly use all other pertinent information as input into the model.
Action sets and action: Third, in each potential state of the system, it is necessary to determine what actions are available to the decision-maker [8]. The set of all possible actions in state st by term, 𝐴t𝑠tt.
Transition probabilities: Fourth component, if it did not consider the system’s evolution, an MDP would be a poor model for an SDP. Based on the present state and behavior, the transition probabilities determine the likelihood with which each potential state is visited at the next decision epoch [9]. To return to the inventory model again, the probability of change depends on the possibility of new demand and the action taken.
The next state is determined by st+1 = st+at-dt.
Where dt is a random variable representing new demand.
Cost functions or reward: Finally, taking a given action may result in a cost function or reward in a given state. It differentiates a good action from a poor one.
The reward function can be written by,
r(St, at, St+1) = f ([St + at – St+1]+) - 0(at) - h(st)
Here, O(a) represents the cost of ordering, h(st) signifies the cost of holding (if st is positive) or the cost of stocking (if it is negative), and f(st+at-stt+1) is the pivotal revenue from the procedures performed [10].
The above five components define an MDP model. The next step is to determine the best policy for the next decision.
In MDP, an important property that needs to be addressed is the Markov property. It states that the impact of every action occupied in each state depends on the state and not upon earlier history and knowledge.
In MDP, policy π is mapping property from state toward actions:
π: S →A, policy determines every one process to proceed an action in every state respectively.
Reward value function: Reward value obtained starting from states and policy π. It is termed the state of the function value [11].
Where
P(s,π,s) is the probability of transition initially from state s and termination after policy π on states’.
R(s,π,s) is estimated to receive rewards when the transition has been followed.
γ a discount element.
The discount element in MDP, represented as γ ∈ (0,1), shows which part of the future reward vanished as compared to the present reward [12].
An optimal policy π is controlling action a ∈ A, which produces the function of max state value and is defined through the Bellman Equation for Optimality:
The optimal strategy can be achieved by solving the problem with Bellman Equation and MDP.
The cost impact on optimal policy: In the MDP, the optimal policy is controlled by manipulating rewards. In this model, they implement the cost factor concept and the expected reward as a result of the baseline reward R, subtracting the costs incurred by the activity during the change of state. Action will start with the attacker or defender [13]. Once the cost factor has been incorporated into the calculation, the Bellman equation is used.
Where, due to action a, C(s, a,s) is cost acquired following the state change from s to s. The given equation will help us evaluate the optimal strategy’s cost effect.
As an optimal strategy, the operation of a ∈{Wait, Defend, Reset}that generates the highest value will be chosen.
This section will discuss some applications of the Markov decision model. Table 1 shows the application of a Markov Decision Model.
| Table 1: Application of Markov Decision Model. | |||
| Reference no. | Summary of problem | Objective Function | Comments |
| 1. Population harvesting | |||
| Johnson [14] | Decisions on how many members of a population need to be left to breed for the next year must be taken annually. | Expected return on discounts over a finite number of years. | Actual population data are used, but return functions are assumed. |
| 2. Agriculture | |||
| Reza [15] | Decisions about whether or not to apply treatment to protect a crop from pests must be made during the season. The new states depend on rainfall at the next decision-making stage. |
Planned expense, irrespective of the impact of pests, during the season. | Accurate data are used. The problem is a dynamic process and is solved via successive approximations. |
| 3. Inspection, maintenance, and repair | |||
| P. G, et al. [16] | Decisions on which module operates in a multi-module system have to be taken. Each module should be tested when the system has been developed, and then which component should be tested. | The estimated time or cost of locating the fault. | The problem is described as a dynamic process. Two models are considered: the first allows a module to be evaluated as a whole, and the second allows only component testing. |
| 4. Finance and investment | |||
| Richard J [17] | An insurance company must make daily decisions about how much to invest and expend on its effective bank balance. The new states depend on the decisions taken earlier. |
Planned bank balance after a limited number of days. | Actual data is used for UK insurance providers. The problem is conceived as a finite-horizon, stochastic dynamic program. |
| 5. Queues | |||
| Yuliya, et al. [18] | Suppose a customer exits or joins a multichannel queueing system. In that case, decisions about the price to be paid for the facility's operation must be made, which will impact the arrival rate. | Planned rewards over an infinite horizon per unit of time, where the rewards include customer payments and negative waiting costs for customers. | The problem is generated from a dynamic program in the finite-horizon semi-Markov. |
| 6. Sales promotion | |||
| Harald J [19] | Decisions must be made regarding the commodity's price discount and duration. | Planned profit over a finite horizon, where profit is gross income net of penalty costs for missing the budget. | The problem is conceived as a finite-horizon stochastic dynamic program. No study is being attempted. |
| 7. Search | |||
| Zhang [20] | Decisions must be made regarding which locations to search for a target. The new states rely on information from the search decision at the next decision epoch. | Expected costs before the goal is set, where the related costs are search costs and negative reward costs. | The problem is formulated as an absorbent-state stochastic dynamic program. The effects of structural policy are achieved. |
| 8. Epidemics | |||
| Conesa D, et al.[21] | Decisions have to be made in an outbreak situation. The states at each decision epoch are the numbers in the population who are infected and can transmit the disease. | The expected cost during the epidemic period is irrespective of the social cost of the epidemic. | A remarkable transformation converts the continuous time problem into a finite-state stochastic dynamic program. |
The Markov decision process is a model of anticipated results. Like a Markov chain, the model endeavors to foresee a result based on the data given by the present status. Be that as it may, the Markov decision process consolidates the attributes of activities and inspirations. At each step during the cycle, the decision maker may select to take an action available in the current state, moving the model to the subsequent stage and offering the decision maker a reward. Figure 1 shows the working flow of the Markov decision process.
Figure 1 shows that an agent perceives the environment, takes the action, and moves to the next state. Agent receives a positive reward against the correct action and a negative reward against the wrong action.
The big challenge facing MDP theory has been called the curse of dimensionality. The state space size in many applications is too large to allow even modern computing capabilities to solve the MDP model directly. In an attempt to solve larger MDP models, a field of research called Approximate Dynamic Programming (ADP) has evolved in recent decades.
In the past, researchers have used the Markov decision process to solve optimization problems. Some of the techniques are discussed here. In this article, we discuss the use and outcomes of MDP in different application areas. In this section, we compare MDP-based optimization techniques. This study collected papers on MDP from Google Scholar and discussed the details of each method. It evaluated each method based on several factors, such as the focus area, strengths, and weaknesses. This study categorized the existing method based on an application area. In Table 2, we discuss the enhancement of MDP and Reinforcement learning. Table 3 discusses the use of MDP in industry manufacturing and document retrieval. MDP is also used in the Finance and investment application area to identify the risk factors discussed in Table 4. In agriculture, water utilization is an essential factor for irrigation systems. MDP is used in agriculture application areas to make irrigation systems efficient. The researcher has previously worked on this area using MDP, which we discussed in Table 5.
| Table 3: Use of MDP in industry manufacturing and document retrieval. | |||||
| Reference no. | author/date | focus area and problem | methodology | Strength and result | Journal/Conference |
| 31 | Taylor W. Killian/2016 | The author addresses the voltage violation problem using an optimal charging strategy model based on reinforcement learning. | In the situation of uncertain EV users' behaviors, the author uses the MDP approach | Ding verifies that this method can strictly guarantee voltage protection compared to conventional approaches. | 30th Neural Information Processing Systems Conference, Barcelona, Spain (NIPS 2016). |
| 32 | Shuang Qiu/2020 | In this paper, the author proposes a new primary-dual upper confidence algorithm for losses received and budget consumption control. | In this work, an upper confidence primal-dual algorithm is proposed | A new high-probability drift analysis of Lagrange multiplier processes is presented in this analysis. | 34th Neural Information Processing Systems Conference, Vancouver, Canada (NeurIPS 2020). |
| 33 | Zeng Wei/ 7 Aug 2017 | The author Proposed a Novel Model based on MDP to rank the document for the information retrieval system. | To train model parameters, the REINFORCE policy gradient algorithm is used. | MDPRank may outperform the state-of-the-art baselines. | “LETOR” benchmark datasets are used. |
| 34 | Ersin Selvi/2018 | In this work, the Radar communications coexistence problem is examined | To solve the optimization problem, apply reinforcement learning | The proposed approach minimizes interference | IEEE |
| 35 | Aiwu Ruan/2019 | In this paper, the author addresses the issue of SRAM FPGA interconnect resources coverage. | Reinforcement learning was used to tackle the issue of complete coverage issues for FPGAs | The experimental results show that configuration numbers can be optimized | IEEE Transactions on Circuits and Systems |
| 36 | Giuseppe De Giacomo /202 | This study uses Markov Decision Processes to optimize device assignments in Digital Twins, adapting to uncertainty and improving cost and quality. | The methodology employs Markov Decision Processes inspired by Web service composition to automatically assign devices to manufacturing tasks. | Their proposed approach demonstrates optimal policies for device assignment in manufacturing tasks. | Computers in Industry |
| Table 4: Use of MDP in finance and investment. | |||||
| Reference no. | Date/Author | Focus area | Methodology | Results and strength | Journal/ Conference |
| 37 | Chiao-Ting Chen | The author proposed a professional trading strategies system for finance investment in this work. | The author used an agent-based reinforcement learning approach. To improve the convergence, the trained model is transferred to DPN. | The experimental results show that this system reproduces almost eighty percent of trading decisions. | 2018 IEEE International Conference on Agents (ICA) |
| 38 | Thomas W. Archibald | In this study, the writer analyzes the contract between the investor and the entrepreneur. | The MDP-based approach is used. | The theoretical results conclude that the investor and the entrepreneur are better off under the contract, and they also observe that the entrepreneur will take risky action when payment becomes harder | Annals of Operations Research |
| 39 | Yang Bai | Determine the investment strategy for gas exploration under such uncertainty | They proposed MDP to determine investment strategy. | They conclude the project is only feasible if the production capacity is more than 8.55 billion cubic meters. They also show that financial subsidies are beneficial for gas investments. | Energy Polic |
| 40 | Ali Nasir | They calculate the optimal decision policy for the trade of options, taking American options trading systems. | Markov decision process is used. MDP takes the conditional probabilities of the prices from various features. | The results conclude that there is an advantage for the financial community but not limited to the investors. | Computational Economics |
| Ref1 | Ben Hambly | This study reviews recent developments and applications of reinforcement learning approaches in finance. | This paper introduces Markov decision processes as the foundation for reinforcement learning approaches in finance. | The study highlights successful applications of reinforcement learning algorithms in financial decision-making | Mathematical Finance |
| Table 5: Use of MDP in Agriculture. | |||||
| Reference no. | Author/ Date | Focused Area | Methodology | Results and strength | Journal /Conference |
| 41 | Alan Marshall/2018 | Generic irrigation system for efficient use of water in agriculture | MDP is used for creating automatic and precise irrigation | Experimental findings conclude that this approach outperforms as compare to threshold irrigation techniques by 40% | IEEE Conference |
| 42 | Fanyu Bu/2019 | Introduced smart agriculture IoT-based system which contains four layers: Data collection, data transmission, edge computing, and cloud computing layers |
In this work, DRK is combined within the cloud layer to make decisions intelligently | They discuss the latest reinforcement learning models’ algorithms | Future Generation Computer Systems |
| 43 | Tran Kim Toai/2019 | In this work, they give an efficient water utilization approach for agricultural soil land | They used MDP for efficient utilization of water in agriculture | By using this approach, water is supplied to the plants in good time. MDP utilizes 63% water and energy as compared to a threshold level | IEEE conference |
| Ref1 | Weicheng Pan | This study focuses on designing a cooperative scheduling approach based on deep reinforcement learning to minimize makespan. | The methodology models agricultural machinery scheduling as an asymmetric multiple-traveling salesman problem with time windows. | The experimental results demonstrate that their proposed approach significantly outperforms existing modified baselines | Agriculture |
Cloud computing is an emerging area of computer science. Efficient use of energy and data offloading is a problem in cloud computing. Researchers use MDP to solve data offloading issues, which we discussed some work in Table 6. In self-driving cars, a based approach is used for decision-making. In Table 7, we discussed the literature on the based approach in self-driving vehicles. The MDP-based framework is also used in management and maintenance areas. We discussed some literature on the topic of maintenance in Table 8.
| Table 6: Use of MDP in cloud computing and computer networks. | |||||
| Reference no. | Date/ Author | Focused area and problem | Methodology | Results and strength | Journal/Conference |
| 44 | Dongqing Liu/2017 | They solve data offloading problems in mobile cloud computing | They used Hybrid offloading schemes to solve offloading problem | The experimental results show that this proposed approach solves the problem with minimal cost. | IEEE Conference |
| 45 | Mengyu Li/2020 | In this work, the author solves an ambulance offloading problem for the Emergency department. | MDP-based policy iteration algorithm is used in this work | This study significantly reduces the AOD time for bed patients | Omega |
| 46 | Juan Parras/2019 | They address two WSN problems: the problem of optimality and the problem of ad-hoc defense | They used MDP and DRL as frameworks. | An attacker, by using the MDP tool, will successfully exploit these problems and also degrade the defense system | Expert Systems with Applications |
| 47 | Xiaobin Li/2020 | Introduce the machine matching tool for single manufacturing task | MDP and cross-entropy-based approaches are used | The experimental results of the proposed method show its superiority and usability. | Robotics and Computer Integrated Manufacturing |
| 48 | Zhihua Li/2019 | In this work author addresses the problem of overload threshold selection to determine whether the host node is overloaded or not | In this work, they Modeled overload threshold selection as an MDP | The experimental results show that the overload threshold is selected adaptively selected | Cluster Computing |
| 49 | Shamim Yousefia/2020 | In this paper, the mobile software agent concept is introduced for data aggregation on the Internet of Things | This work is divided into two stages there are: cluster the devices and organize the cluster heads using the Markov decision process | The experimental results show the proposed approach improves data transmission delay, energy consumption, and reliability of the devices | Ad Hoc Networks 98 |
| 50 | Laurent L. Njilla/2017 | In this study, Resource allocation for cyber security is investigated in terms of recovery and agility | They proposed the Markov decision process as a framework for resource reallocations | The experimental results conclude that the optimal allocations take the gains from investing in the recovery component | IEEE conference |
| Ref1 | Behzad Chitsaz /2024 | This study focuses on developing a multi-level continuous-time Markov decision process (CTMDP) model for efficient power management in multi-server data centers. | The methodology involves developing a multi-level continuous-time Markov decision process (CTMDP) model based on state aggregation. | The simulation results show that the proposed multi-level CTMDP model achieves a near 50% reduction. | IEEE Transactions on Services Computing |
| Table 7: Use of MDP in self-driving cars. | |||||
| Reference no. | Date/ Author | Focused area and problem | Methodology | Results and strength | Journal/Conference |
| 51 | Jingliang Duan/2019 | In this work, Jingliang Duan at. el introduced the hierarchical RL technique for decision-making in self-driving cars, which is not | They first divide the driving task into three parts: left lane change, right lane change, and driving in the lane, and then learn the sub-policy for each maneuver using hierarchical reinforcement learning | This method is applied to a highway scenario. Experiments conclude that this approach realizes safe and smooth decision-making. | IET Intelligent Transport Systems |
| 52 | Mohsen Kamrani /2020 | In this work, the author understands driving behavior in terms of maintaining speed decisions, acceleration, and deceleration | Individual drivers’s reward functions are estimated using the multinomial logit model and used in the MDP framework. The value iteration algorithm is used for policy-obtaining | The experimental results show that the driver prefers to accelerate when the number of objects around the host is increasing | Transportation Research |
| 53 | Xuewei Qi/ 2018; | The energy management system is introduced to learn autonomously optimal fuel split between the traffic environment and the vehicle | A deep Reinforcement learning-based approach has been applied to energy management in autonomous vehicles. | The experimental findings demonstrate that this DQN model saved 16.3% of energy as compared to conventional binary control strategies. | Transportation Research Part |
| 54 | Shalini Ghosh/ 2018 | Shalini Ghosh et. al., introduced a paradigm to make machine learning models more trustworthy for self-driving cars and cybersecurity. | They applied MDP as the underlying dynamic model and outlined three paradigm approaches: Data repair, model repair, and reward repair | They demonstrate their approaches to car controllers for obstacle avoidance and query routing controllers. | IEEE Conference |
| Ref1 | YUHO SONG/2023 | This study proposes a behavior planning algorithm for self-driving vehicles, utilizing a hierarchical Markov Decision Process (MDP). | The methodology employs a hierarchical Markov Decision Process (MDP) with a path planning MDP that generates path candidates based on lane-change data and speed profiling. | Simulation results demonstrate the effectiveness of the proposed algorithm in various cut-in scenarios. | IEEE Access |
| Table 8: Use of MDP in Maintenance. | |||||
| Reference no. | Date/ Author | Focused area and problem | Methodology | Results and strength | Journal/Conference |
| 55 | Mariana de Almeida Costa/ 2020 | In this work, the author estimates the survival curve and wheel wear rates of Portuguese train operating company | Markov decision-based framework is applied to find the optimal policy. | The experimental results conclude that training operating companies in practice might benefit from using policy. | Wiley and Francis |
| 56 | Yinhui Ao/2019 | This paper proposed a solution to the integrated decision problem of maintenance and production for the semiconductor production line | They developed a dynamic maintenance plan based on MDP, and then the decision model of production scheduling was put forward to the entire semiconductor line | The experimental results show that this method enhances system benefits and usability of critical components. | Computers & Industrial Engineering |
| 57 | Ayca Altay/2019 | In this article, Ayca Altay at. el present a new technique to predict geometry and rail defects and integrate prediction with inspection | They proposed a new technique, a hybrid prediction methodology, and a novel use of risk aversion. The discounted MDP model is used to find the optimal inspection and maintenance scheduling policies | The experimental results showed the highest accuracy rate in effective long-term scheduling and prediction | Transportation Research |
| Ref0 | Giacomo Arcieri /2024 | This study combines deep reinforcement learning with Markov Chain Monte Carlo sampling to robustly solve POMDP | They jointly infer the model parameters via Markov Chain Monte Carlo sampling and solve POMDPs for maintaining railway assets. | The experimental results show that the RL policy learned by their method outperforms the current real-life policy by reducing the maintenance and planning cost for railway assets | Machine Learning |
Enhancement of MDP and reinforcement learning: In this paper, Chi Cheung [22] addresses the issue of undisputed reinforcement learning in Markov decision-making processes in a non-stationary environment. First, he generates a Sliding Window upper confidence bound to the algorithm of Confidence Widening and generates his dynamic regret bound by knowing the budget for variation. To achieve the same dynamic regret without knowing the budgets for variation. It also suggests that the Bandit over RL algorithm be recursively tuned to the sliding window upper-confidence bound algorithm. The main feature of this algorithm is the new confidence-enhancing method, which gives added optimism to the design of the learning algorithms. In this paper [23], the Authors updated the HiP-MDP framework as the existing framework had a critical issue in that embedding uncertainty was designed independent of the agent’s state. Killian extends the framework to develop personalized medicine strategies for HIV treatment. Experiment results show that HiP-MDP effectively learns treatment strategies that comply with the naive “personally-tailored” basis but rely on much fewer data. HiP-MDP also performs better with the baseline one-size-fits-all. This paper proposes a general theory of regularized Markov decision processes [24], classifying these approaches in two ways. He considers a large class of regularization and then transforms these classes into two policy iterative processes and value iteration. This approach enables general algorithmic schemes to be analyzed for error propagation. Chen-Yu [25] proposed two model-free algorithms for learning infinite-horizon average reward MDP. The first approach solves the discounted incentive problem and achieves O (T 2/3). The second algorithm includes recent O (T 1/2) function selection advances. In this paper, Wachi [26] proposes an SNO-MDP algorithm that searches and improves Markov decision processes within unfamiliar safety constraints. In this method, an agent learns safety constraints and then enhances the collective reward in the certified safe region. It provides imaginary assurances of satisfaction with the safety and regularity constraints. Experiments show the efficiency of SNO-MDP using two tests: one test uses unreal data in an open environment called GP-SAFETYGYM, and the other test simulates Mars surface exploration through actual observation data. Ensure robustness in Markov decision processes (MDP) is addressed in an article by the Author to ensure robustness concerning unexpected or adversarial system behavior by using an online learning approach [27]. In this paper, Tuyen P. Le studied hierarchical RL in the POMDP, in which the tasks are only partially measurable and possess hierarchical properties. A hierarchical deep reinforcement learning approach is proposed in the hierarchical POMDP. A deep hierarchical RL algorithm is proposed for MDP and POMDP learning domains. They evaluate the proposed algorithm using a variety of challenging hierarchical POMDPs [28]. In Contextual Markov Decision Processes, environments chosen from a possibly infinite set agent have an episodic sequence of tabular interactions. The parameters of these environments depend on the background vector available to the agent at the beginning of each episode. In this thesis, the Author proposed a noregret online RL algorithm in the setting where the MDP parameters are extracted from the context using generalized linear models. This method relies on efficient web updates and memory efficiency [29]. A sparse Markov decision technique with novel causal sparse Tsallis entropy regularization is proposed. The suggested policy regularization causes a sparse and multimodal optimal policy distribution of the sparse MDP.
In comparison to soft MDPs that use the regularization of causal entropy, the proposed sparse MDP. They show that a sparse MDP’s output error has a constant bound, while a soft MDP’s error increases. Where the performance error is caused by the time of implementation of the regularization. In tests, they use sparse MDPs to reinforce learning challenges. The method proposed outperforms current methods in terms of convergence speed and efficiency [30]. Table 2 shows the comparative analysis of Markov Decision Process Model.
Tao Ding proposes [31] using the MDP approach in the scenario of uncertain EV users’ behaviors. Ding identifies that this approach strictly guarantees voltage protection, but the conventional stochastic approach cannot. The MDP and the online learning techniques can fully consider the temporal correlations. Shuang Qiu [32] proposes a different upper confidence primal-dual algorithm. He only needs to sample from the transition model. The proposed algorithm achieves the upper bounds of both the constraint and regret violation. His proposed model does not require transition models of the MDPs.
In this article, the author addresses the problem of document ranking for information retrieval. The basis of MDP, referred to as MDP Rank is a novel learning to rank the novel by author. Rank is a document for the corresponding position in the learning phase of MDP. The construction of a document ranking is considered sequential decision-making; each corresponds to an action of selecting. The model parameters are adopted to train the policy gradient algorithm of REINFORCE [33]. In this article, they examine an MDP and then apply reinforcement learning to solve the optimization problem of the radar-communications coexistence problem by modeling the radar environment. They demonstrate how the reinforcement learning and MDP framework can be used to help the radar predict which bands the interferer will use and utilize bands that minimize interference, which will the radar optimize between range resolution and SINR [34]. SRAM FPGAs have been an obstacle to the complete coverage of integrated tools for science and engineering topics such as testing diagnostics and fault tolerance. SRAM FPGAs have been an obstacle to the complete coverage of integrated tools for science and engineering topics such as testing, diagnostics, and fault tolerance. The simple requirement to cover as many interconnect resources as possible with minimum configuration numbers should be followed. FPGAs have been achieved by resolving the MDP with Dynamic Programming for Maximum Interconnect Resource Coverage. Experimental findings show that configuration numbers can be configured to reach a theoretical number with maximum coverage achieved, and the technique is also applicable to NP-complete issues such as FPGA checking. [35]. In episodic loop-free Markov processes (MDPs), where the error function may differ dynamically between episodes, Rosenberg perceives online learning, and the transition function is unknown to the learner. He shows the regret of O (L|X|(|A|T) 1/2 using the methodology of entropic regularization. Rosenberg’s online algorithm has been implemented, which enables the initial oppositional MDP model to be extended to handle curved performance criteria and also improves the previous limit of regret [36]. Table 3 shows the comparative analysis of MDP in manufacturing and document retrieval in industry. Tables 4,5 present a comparative study of MDP for finance and agriculture. Tables 6-8 describe the comparative analysis of MDP for cloud computing and computer networks, self-driving cars, and maintenance, respectively.
This survey comprehensively reviews Markov decision processes (MDPs) application in various optimization domains such as the manufacturing industry, document retrial, cloud computing, networks, agriculture, finance, maintenance, and planning. The comparative analysis of past works highlights the effectiveness of MDP-based methods in handling complex decision-making tasks. MDPs offer robust solutions for dynamic and uncertain environments. Besides the advantages of a MDP, some challenges still need to be addressed. These challenges are the scalability of MDP, robustness to uncertainty, explainability, and interpretability. Future research can focus on developing scalable MDP algorithms and needs to enhance the robustness by utilizing the probabilistic models and Bayesian method. It helps to address the uncertainty in transition probabilities and reward functions. There is also a need to focus on the explainability and interpretability of MDP-based models because they provide insights that can help decisions.
Dynamic programming has different applications in real-world problems. We used Dynamic programming, where we had multiple solutions and selected the best from the various solutions. Dynamic Programming’s algorithm Markov decision process is used in decision making. In this work, we surveyed MDP-based optimization algorithms that can be used to solve optimization problems. We briefly discussed the application areas where the Markov decision process is used to learn an optimal policy for decision-making, like self-driving cars. In autonomous vehicles, the MDP-based approach makes proper decisions at the right time to avoid obstacles like pedestrians and other vehicles. MDP solves data offloading problems and resource allocations in computer networks and cloud computing. From the Literature survey, we conclude that MDP techniques are used in robotics, self-driving cars, radar tracking, finance and investment, agriculture, and fault tolerance in industry manufacturing for taking optimized action in an environment.
We make a comparative analysis of the focused problem area, methodology, and strength of the results. In the future, we may improve this survey by using another matrix for comparison, such as drawbacks/weaknesses of techniques. In our survey, we added twelve application areas of MDP, but in the future, we may add more application areas like forestry management and flight scheduling. We classify our literature based on application areas taxonomy, but in the future, we may classify this literature on other types of taxonomy [58-63].
Khan QA. Exploring Markov Decision Processes: A Comprehensive Survey of Optimization Applications and Techniques. IgMin Res. Jul 04, 2024; 2(7): 508-517. IgMin ID: igmin210; DOI:10.61927/igmin210; Available at: igmin.link/p210
次のリンクを共有した人は、このコンテンツを読むことができます:
Address Correspondence:
Qazi Waqas Khan, Department of Computer Engineering, Jeju National University, Jejusi 63243, Jeju Special Self-Governing Province, Republic of Korea, Email: [email protected]
How to cite this article:
Khan QA. Exploring Markov Decision Processes: A Comprehensive Survey of Optimization Applications and Techniques. IgMin Res. Jul 04, 2024; 2(7): 508-517. IgMin ID: igmin210; DOI:10.61927/igmin210; Available at: igmin.link/p210
Copyright: © 2024 Khan QW This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
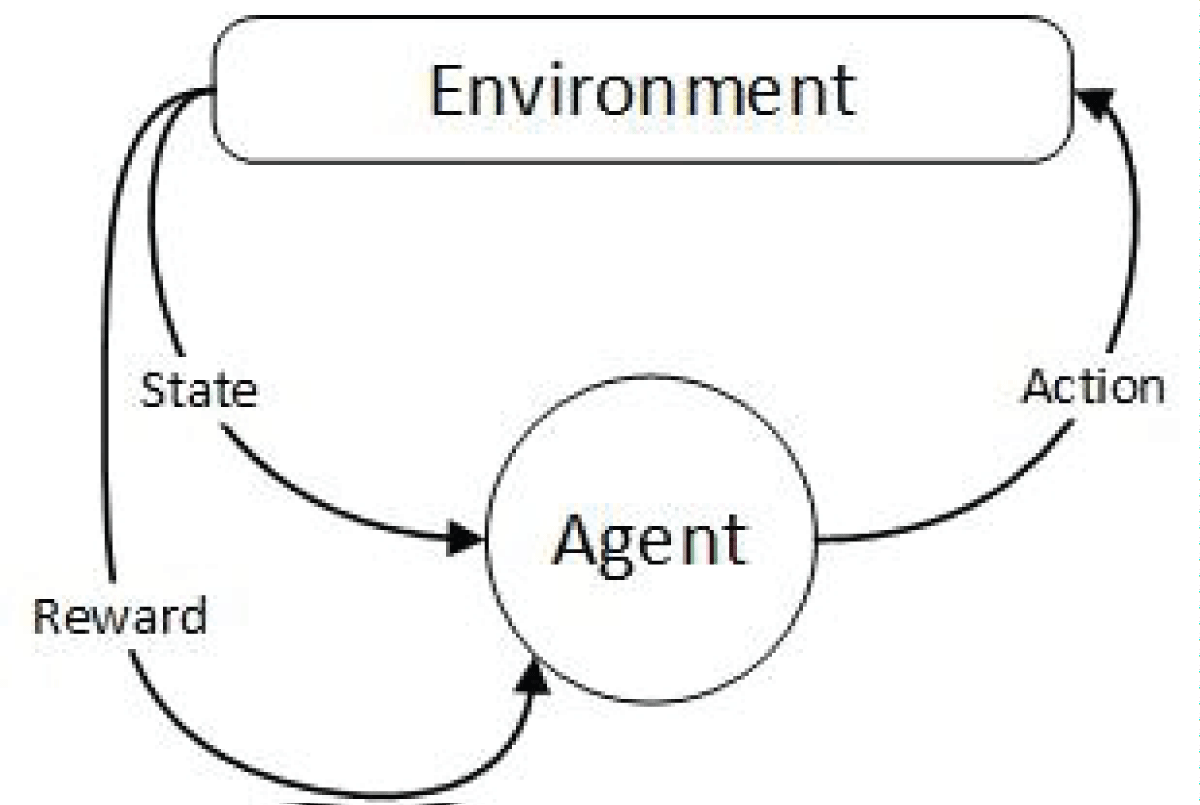 Figure 1: Working Flow of MDP....
Figure 1: Working Flow of MDP....
 Figure 1: Working Flow of MDP....
Figure 1: Working Flow of MDP....