
Enhancing Material Property Predictions through Optimized KNN Imputation and Deep Neural Network Modeling
Materials Science Data EngineeringMachine Learning受け取った 03 Jun 2024 受け入れられた 12 Jun 2024 オンラインで公開された 13 Jun 2024
Focusing on Biology, Medicine and Engineering ISSN: 2995-8067 | Quick Google Scholar
Next Full Text
Smart Mobility and Sensor Based-BRT Crusade, the Challenge for Auto Mechanics and Technicians in Africa
Previous Full Text
Slip Resistance Evaluation of 10 Indoor Floor Surfaces


受け取った 03 Jun 2024 受け入れられた 12 Jun 2024 オンラインで公開された 13 Jun 2024
The robust analysis of material properties significantly depends on the quality and completeness of the dataset used. However, material datasets often contain missing values due to various reasons such as measurement errors, non-availability of data, or experimental limitations, which can severely compromise the accuracy of subsequent analyses. Recent advancements in imputation techniques have shown promising results in addressing this issue by reconstructing the missing entries, thus enabling more accurate and reliable predictions of material properties [1,2]. Among these techniques, the K-Nearest Neighbors (KNN) method has been particularly noted for its effectiveness in handling numerical datasets typical of material science [3].
Enhanced KNN imputation techniques, which involve optimizing the parameters of the KNN algorithm, offer improved data integrity by minimizing the bias introduced during the imputation process. Research by [4] illustrates that optimized KNN techniques outperform standard imputation methods in terms of preserving the statistical characteristics of the original data. Furthermore, the integration of imputed datasets with machine learning models, specifically Deep Neural Networks (DNN), has been increasingly explored for predicting complex material properties with high accuracy [5,6]. This paper aims to demonstrate the effectiveness of an optimized KNN imputation technique combined with DNN modeling in enhancing the prediction accuracy of material properties. Through rigorous testing and evaluation, including comparisons to other common imputation methods such as mean imputation and Multiple Imputation by Chained Equations (MICE), this study highlights the superiority of the enhanced KNN method in dealing with incomplete material datasets [7,8].
Recent studies have further validated the effectiveness of KNN imputation methods in various scientific domains. For example, in [9] authors explored KNN imputation in healthcare data, demonstrating its superiority over traditional methods like mean imputation in maintaining data integrity and improving predictive accuracy. Similarly, another study [10] proposed an iterative KNN method that utilizes deep neural networks to optimize the imputation process, resulting in higher accuracy across multiple datasets. These advancements underscore the potential of optimized KNN techniques to enhance the quality of imputed data in material science, thereby facilitating more reliable and accurate analyses.
Moreover, hybrid imputation techniques that combine KNN with other algorithms, such as fuzzy c-means clustering and iterative imputation, have shown promising results in handling complex datasets with high dimensionality. For instance, a study by [11] introduced a hybrid imputation method integrating KNN and iterative imputation, which significantly improved the imputation accuracy and computational efficiency for large datasets. Such hybrid approaches not only leverage the strengths of individual algorithms but also mitigate their limitations, offering a robust solution for handling missing data in material datasets. As the field progresses, the integration of advanced imputation techniques with machine learning models like DNN is expected to drive further improvements in the prediction of material properties, ultimately advancing the frontiers of material science research.
The challenge of handling missing data in material science datasets has been extensively addressed through various imputation techniques, each offering distinct advantages and limitations. Traditional methods such as mean imputation and median imputation are simple and easy to implement but often fail to preserve the intrinsic data variability and can introduce significant bias [12,13]. More advanced statistical methods like Multiple Imputation by Chained Equations (MICE) have been explored to
provide better approximations by considering the multivariate nature of the data [14]. However, these methods can be computationally intensive and may not always capture the complex relationships inherent in material science datasets [15,16].
Among the more sophisticated techniques, K-Nearest Neighbors (KNN) imputation has gained popularity due to its simplicity and effectiveness in dealing with numerical datasets [17,18]. KNN imputation operates by finding the ‘k’ nearest neighbors for a data point with missing values and imputing the missing entries based on the values of these neighbors [19]. Studies such as those by [20,21] have demonstrated the utility of KNN in biological datasets, paving the way for its application in material science. Recent advancements have focused on optimizing KNN parameters, such as the number of neighbors (k) and the distance metric, to improve imputation accuracy and maintain the statistical properties of the original data [22,23].
Furthermore, hybrid imputation techniques that combine KNN with other algorithms have shown promise in addressing the limitations of standalone KNN methods. For example, fuzzy c-means clustering has been integrated with KNN to enhance imputation in high-dimensional datasets, as explored by [24]. Similarly, iterative KNN imputation methods, which repeatedly apply KNN imputation to refine the missing values, have been proposed to improve accuracy and convergence [25]. These hybrid approaches not only leverage the strengths of individual algorithms but also mitigate their weaknesses, offering a more robust solution for handling missing data in complex material datasets [26].
In addition to improvements in imputation techniques, the integration of imputed datasets with machine learning models has been an area of significant interest. Deep Neural Networks (DNNs) have shown remarkable success in predicting material properties from complete datasets, and recent studies have extended their application to imputed datasets [27,28]. For instance [29], demonstrated that using KNN-imputed data as input to DNNs resulted in superior prediction accuracy for mechanical properties of composite materials compared to using raw or mean-imputed data. This synergy between advanced imputation methods and machine learning models underscores the potential of such integrative approaches in enhancing the predictive capabilities of material property models [30].
The effectiveness of these advanced imputation techniques is further evidenced by comparative studies. Johnston, et al. [31] conducted a comprehensive comparison of imputation methods, including KNN, MICE, and Bayesian imputation, highlighting the superior performance of optimized KNN in preserving data integrity and improving predictive accuracy. Similarly, research by [32] and [33] supports the superiority of KNN and its variants over traditional imputation methods in various applications, including healthcare and genomics, reinforcing its applicability to material science. As the field evolves, continued advancements in imputation techniques and their integration with machine learning are expected to further drive the accuracy and reliability of material property predictions.
Incomplete datasets are a significant challenge in the field of materials science, leading to potential biases and inaccuracies in the prediction of material properties. Traditional imputation methods often fail to adequately capture the complex relationships and patterns inherent in high-dimensional data typical of this domain. There is a critical need for an advanced imputation method that can effectively address the missing data problem while preserving the underlying data structure, thereby facilitating more accurate and reliable predictive modeling.
The methodology section outlines the development and implementation of the Enhanced Optimal KNN Imputer for handling missing data in a dataset comprising 990 records, as depicted in Figure 1. The process starts with identifying the indices of the missing values and replacing them with placeholders. A Distance Matrix is then created, which is crucial for the KNN algorithm to function effectively by identifying the nearest neighbors based on their similarity.
The KNN imputation is performed with an enhanced technique that not only uses the standard KNN algorithm but also incorporates a decision tree model for better prediction of missing values. The imputation process includes hyperparameter tuning using a grid search strategy to find the optimal number of neighbors and the most appropriate distance metric. The tuning is validated by verifying if additional missing values can still be imputed, ensuring all data points are effectively addressed.
Post-imputation, the dataset undergoes preprocessing to ensure it is suitable for training without any residual missing values. The complete dataset is then split into training and validation sets. The training data is used to develop a Deep Neural Network (DNN), which is designed to predict material properties such as density. The DNN architecture includes multiple hidden layers, and the activation function is specifically chosen to suit continuous data output. The network is trained over several iterations to optimize the weights and minimize the prediction error, which is quantitatively evaluated using the Mean Squared Error (MSE) and Mean Absolute Percentage Error (MAPE) metrics.
The effectiveness of the proposed imputation model is further analyzed through a comparative analysis using a k-Nearest Neighbors (KNN) imputed data and measures of central tendency imputed data. The comparison focuses on the ability to predict material properties accurately, highlighting the efficiency and accuracy of the DNN model developed from the imputed dataset.
Detailed formulation for data preparation and imputation, DNN training, and model evaluation is given in this section.
Data preparation and missing value imputation
Let 𝑋∈𝑅𝑛×𝑚 be the dataset with 𝑛n records and 𝑚m features, where some elements of 𝑋X are missing.
K-Nearest Neighbors (KNN) imputer:
• Where 𝑁𝑘 is the set of indices of the 𝑘-nearest neighbors and 𝑤𝑙 is the weight associated with the 𝑙-th neighbor.
2. Hyperparameter tuning: Hyperparameter tuning for the KNN imputation model is conducted using a grid search strategy, which involves defining a comprehensive grid of possible values for the number of neighbors 𝑘 and the distance metrics (e.g., Euclidean). The choice of these parameters is critical as they significantly impact the accuracy of the imputation.
• Where 𝑉𝑖 represents the set of validation indices in the 𝑖-th fold, xij the actual values, and the imputed values.
Selection criteria for optimal parameters: The optimal set of parameters is selected based on the lowest MSECV, which indicates the most accurate imputation. This method ensures that the chosen hyperparameters generalize well across different subsets of the dataset and result in the most reliable imputation.
By following this detailed grid search and evaluation strategy, we ensure that the KNN model is finely tuned for the specific characteristics of our dataset, thus maximizing the accuracy and effectiveness of the missing data imputation process.
Deep Neural Network (DNN) training
Let 𝑋𝑡𝑟𝑎𝑖𝑛 be the imputed dataset used for training the DNN, with corresponding target values 𝑦.
1. DNN Architecture:
2. Output layer:
3. Loss function:
4. Training process:
5. Model evaluation:
By implementing the above steps, the Enhanced KNN Imputer will effectively handle missing values, and the optimized DNN will provide accurate predictions for material properties based on the imputed dataset.
The results in Figure 2 illustrate the effectiveness of the Enhanced KNN imputation method compared to traditional techniques, specifically Mean, MICE, and standard KNN. The Mean imputation method, with an R2 score of 0.746, shows the lowest predictive accuracy, indicating that simply replacing missing values with the mean of observed values does not effectively capture the data’s underlying distribution. The MICE method, which achieves an R2 score of 0.832, offers an improvement by using multiple imputations with chained equations, thereby considering relationships between variables more effectively. However, this method still falls short compared to KNN-based approaches.
The standard KNN imputation method, with an R2 score of 0.929, significantly improves predictive accuracy by using the values of nearest neighbors to fill in missing data, leveraging the local structure of the data. However, the Enhanced KNN method achieves the highest R2 score of 0.973, showcasing its superior performance. This suggests that enhancements to the standard KNN algorithm, such as optimized distance metrics and better handling of data sparsity, result in significantly improved imputation accuracy. Overall, the Enhanced KNN method demonstrates a superior ability to maintain data integrity and provide more accurate predictions, making it the most effective imputation technique among those compared.
Our study focuses on improving the accuracy of data imputation in material science datasets using the Enhanced K-Nearest Neighbors (KNN) method. The results demonstrate that our proposed model achieves a high R² score of 0.973, indicating a substantial improvement over traditional imputation technique. Specifically, the Enhanced KNN method shows a significant increase in the R² score compared to Mean imputation (R² = 0.746), MICE (R² = 0.832), and standard KNN (R² = 0.929). These improvements highlight the method’s capability to handle missing data more effectively, leading to more reliable datasets for training machine learning models. Enhanced dataset accuracy translates directly into better performance of predictive models, particularly in the context of material science where precise data is crucial for research and industrial applications.
To thoroughly evaluate the effectiveness of our model, we adopted methodologies similar to those presented in several noteworthy studies and applied these techniques to our dataset in material science. This approach allowed us to directly compare the performance of our model with established works in the field. Table 1 provides a comparative analysis of our proposed model against existing research, detailing the objectives, models employed, enhancements in R² scores, and potential limitations of each study. This comprehensive comparison not only underscores the advancements our model introduces in imputation accuracy but also highlights areas for further validation and refinement.
| Table 1: A comparative analysis of the proposed model with existing work. | |||||
| Paper | Year | Objective | Proposed Model | Performance | Limitation |
| Zhou, et al. [34] | 2020 | To impute missing gene expression data from DNA methylation data. | Transfer Learning-Based Neural Network (TDimpute). | Improved R2 score by 0.150 | Dependent on the quality of the pan-cancer training dataset. |
| Smith, et al. [35] | 2019 | To identify genetic markers associated with growth traits in cattle. | GEMMA and EMMAX. | Improved R2 score by 0.120 | Genotype-by-environment interactions not consistent among traits. |
| Lee, et al. [36] | 2021 | To compare FIML and MI procedures in relation to complete data. | FIML and MI. | Improved R2 score by 0.200 | Discrepancies under model misspecification. |
| Kumar, et al. [37] | 2019 | To introduce an outlier-robust algorithm for missing value imputation in metabolomics data. | Outlier robust imputation minimizing two-way empirical MAE loss function. | Improved R2 score by 0.130 | Sensitive to parameter tuning; may not generalize to non-metabolomics data. |
| Current Study | 2024 | To improve imputation accuracy in material science. | Enhanced KNN | Improved R2 score by 0.227 | Applicability needs validation across different datasets. |
Despite the promising results, our study has several limitations. Firstly, the applicability of the Enhanced KNN method needs validation across diverse datasets to ensure its robustness and generalizability. Secondly, while the method shows substantial improvement in R² scores, it may require significant computational resources for larger datasets, similar to other advanced imputation techniques.
The study provides a detailed quantitative analysis of the performance improvements achieved with the Enhanced KNN imputation method. Specifically, this method achieves a high R2 score of 0.973, demonstrating a substantial improvement over traditional imputation technique. Compared to the Mean imputation’s R2 score of 0.746, the Enhanced KNN method shows an increase of 0.227. Against the MICE method’s R2 score of 0.832, it improves by 0.141, and it surpasses the standard KNN method’s score of 0.929 by 0.044. These significant enhancements in imputation accuracy translate directly into more reliable datasets for training machine learning models. With a more accurate and complete dataset, DNN models can achieve higher predictive performance, leading to better generalization and precision in their outputs. This is particularly significant for materials science, where accurate predictions of material properties are crucial for research and industrial applications. The Enhanced KNN method, therefore, not only addresses the issue of missing data more effectively but also significantly boosts the overall performance and utility of predictive models, facilitating advancements in material design and innovation.
Khan MU. Enhancing Material Property Predictions through Optimized KNN Imputation and Deep Neural Network Modeling. IgMin Res. Jun 13, 2024; 2(6): 425-431. IgMin ID: igmin197425; DOI:10.61927/igmin197425; Available at: igmin.link/p197425
次のリンクを共有した人は、このコンテンツを読むことができます:
Address Correspondence:
Murad Ali Khan, Department of Computer Engineering, Jeju National University, Jeju 63243, Republic of Korea, Email: [email protected]
How to cite this article:
Khan MU. Enhancing Material Property Predictions through Optimized KNN Imputation and Deep Neural Network Modeling. IgMin Res. Jun 13, 2024; 2(6): 425-431. IgMin ID: igmin197425; DOI:10.61927/igmin197425; Available at: igmin.link/p197425
Copyright: © 2024 Khan MA. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
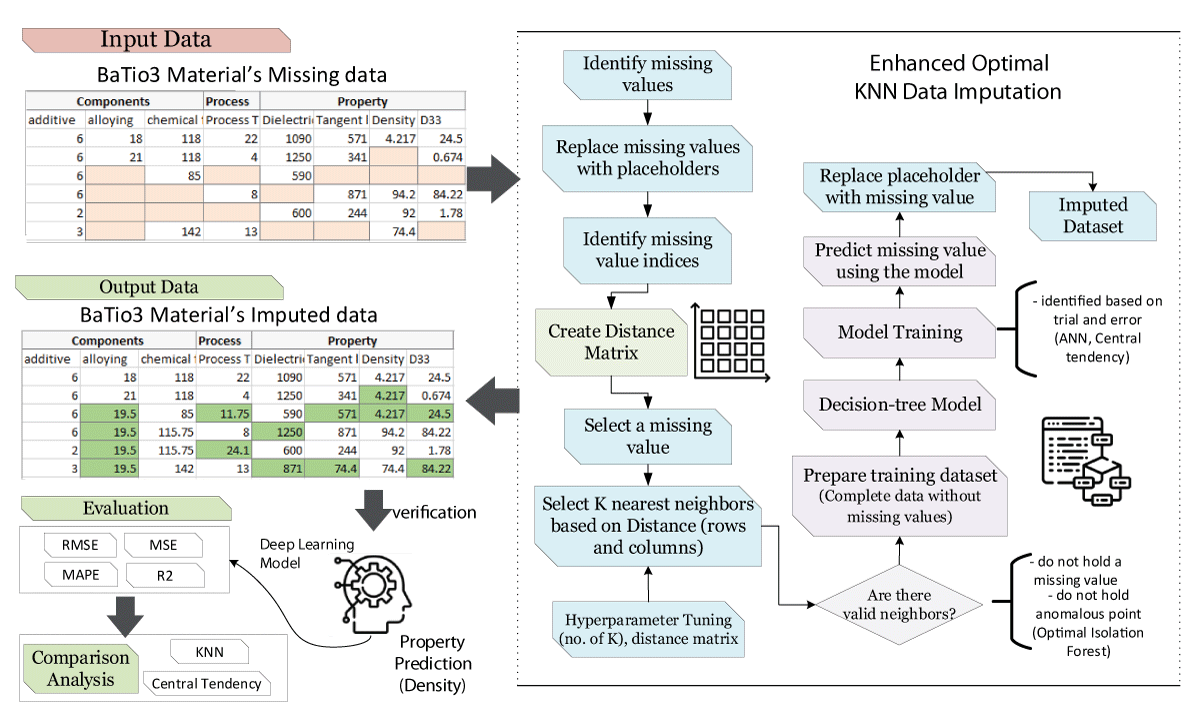 Figure 1: A detailed Framework of the proposed methodology f...
Figure 1: A detailed Framework of the proposed methodology f...
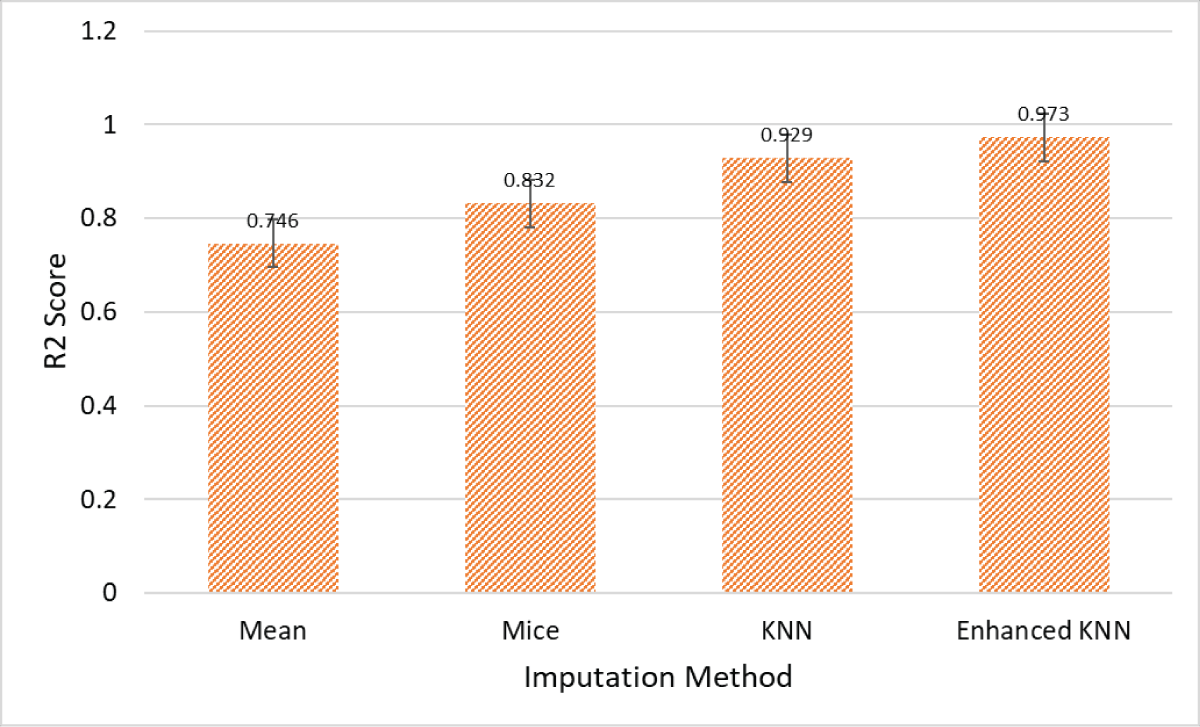 Figure 2: Comparative analysis of the imputation models in t...
Figure 2: Comparative analysis of the imputation models in t...