
Enhancing Missing Values Imputation through Transformer-Based Predictive Modeling
Information Technology Data EngineeringArtificial Intelligence受け取った 08 Dec 2023 受け入れられた 22 Jan 2024 オンラインで公開された 23 Jan 2024
Focusing on Biology, Medicine and Engineering ISSN: 2995-8067 | Quick Google Scholar
Next Full Text
Association and New Therapy Perspectives in Post-Stroke Aphasia with Hand Motor Dysfunction


受け取った 08 Dec 2023 受け入れられた 22 Jan 2024 オンラインで公開された 23 Jan 2024
This paper tackles the vital issue of missing value imputation in data preprocessing, where traditional techniques like zero, mean, and KNN imputation fall short in capturing intricate data relationships. This often results in suboptimal outcomes, and discarding records with missing values leads to significant information loss. Our innovative approach leverages advanced transformer models renowned for handling sequential data. The proposed predictive framework trains a transformer model to predict missing values, yielding a marked improvement in imputation accuracy. Comparative analysis against traditional methods—zero, mean, and KNN imputation—consistently favors our transformer model. Importantly, LSTM validation further underscores the superior performance of our approach. In hourly data, our model achieves a remarkable R2 score of 0.96, surpassing KNN imputation by 0.195. For daily data, the R2 score of 0.806 outperforms KNN imputation by 0.015 and exhibits a notable superiority of 0.25 over mean imputation. Additionally, in monthly data, the proposed model’s R2 score of 0.796 excels, showcasing a significant improvement of 0.1 over mean imputation. These compelling results highlight the proposed model’s ability to capture underlying patterns, offering valuable insights for enhancing missing values imputation in data analyses.
In the ever-evolving data analysis landscape, the challenge of missing values within datasets is a formidable hurdle, impacting the reliability and efficacy of downstream applications []. Addressing this challenge has spurred the development of various imputation techniques, each attempting to reconcile the absence of data points with meaningful estimations. Traditional methods, such as zero imputation, mean imputation, and K-Nearest Neighbors (KNN) imputation, have long been employed. Yet, their efficacy is often limited in capturing complex dataset’s intricate relationships and patterns.
Recognizing the shortcomings of conventional approaches and the imperative to preserve valuable information lost through record removal, this paper introduces an innovative method for missing values imputation. The proposed approach leverages the capabilities of advanced transformer models, which have exhibited exceptional performance in handling sequential data and contextual information. The transformer model is trained to predict missing values based on the inherent contextual dependencies within the dataset, offering a promising alternative to traditional imputation techniques []. Moreover, the utilization of transformer models in missing values imputation represents a paradigm shift from rule-based imputation methods to a more data-driven and adaptive approach []. By harnessing the power of self-attention mechanisms [], the transformer model can effectively capture intricate relationships and dependencies across different features, leading to more accurate predictions of missing values.
This innovative approach is particularly advantageous when dealing with large and complex datasets, where conventional imputation techniques may struggle to capture the nuanced patterns inherent in the data. The transformer model’s ability to consider global context and long-range dependencies ensures a holistic understanding of the dataset, enhancing its capacity to impute missing values in a manner that aligns with the underlying structure of the information []. Statistical imputation techniques employ conventional statistical methods, such as substituting missing values with the mean of available data and utilizing regression models [-].
In addressing missing data in short-term air pollutant monitoring with real-time PM2.5 monitors [], univariate methods like Markov, random, and mean imputations prove superior, especially beneficial in resource-limited contexts. Furthermore, DACMI [] addresses missing clinical data with a shared dataset, revealing that models like LightGBM and XGBoost, coupled with careful feature engineering, excel in imputation performance, emphasizing the importance of balanced model complexity. In scRNA-seq, vital for studying single-cell transcription, addressing high-dimensionality and dropout values is crucial. This study [] evaluates advanced imputation methods, providing insights for selecting appropriate approaches in diverse data contexts and aiding downstream functional analysis. Both the Self-Organizing Map (SOM) [,] and the MLP [] represent additional ML techniques applied for the imputation of missing values.
Furthermore, studies employing the regression approach [] implemented a novel method involving weighted quantile regression to estimate missing values within health data. In another article [], the author introduced a comprehensive case regression approach for handling missing values, employing functional principal components. Iterative regression is used for effective imputation in multivariate data []. Another method Hot-deck imputation, matches missing values with complete values on key variables []. Research is conducted on expectation minimization in handling missing data using a dataset analyzing the effects of feeding behaviors among drug-treated and untreated animals []. Recognizing the insufficiency of merely deleting or discarding missing data [], researchers often turn to employing multiple imputations. Multiple imputation involves leveraging the observed data distribution to estimate numerous values, reflecting the uncertainty surrounding the true value. This approach has predominantly been utilized to address the constraints associated with single imputation [].
Moreover, another study [] evaluates imputation methods for incomplete water network data, focusing on small to medium-sized utilities. Among the tested methods, IMPSEQ outperforms others in imputing missing values in cast iron water mains data from the City of Calgary, offering insights for cost-effective water mains renewal planning. The proposed one-hot encoding method by [] excels in addressing missing data for credit risk classification, demonstrating superior accuracy and computational efficiency, especially in high missing-rate scenarios, when integrated with the CART model. Another work [] proposes a novel imputation method for symbolic regression using Genetic Programming (GP) and weighted K-Nearest Neighbors (KNN). It outperforms state-of-the-art methods in accuracy, symbolic regression, and imputation time on real-world datasets. Conventional techniques for multiple imputations exhibit suboptimal performance when confronted with high-dimensional data, prompting researchers to enhance these algorithms [,]. Likewise, indications exist that exercising caution is advisable when applying continuous-based approaches to impute categorical data, as it may introduce bias into the results [].
Motivated by the need for a comprehensive evaluation, we conduct extensive experiments to compare the performance of our transformer-based imputation against established methods. This comparison extends beyond conventional imputation techniques, encompassing zero [], mean [], and KNN imputations []. In the context of missing value imputation, it is noteworthy that addressing missing values is a common concern among researchers and data scientists. Recent research [] thoroughly compares seven data imputation methods for numeric datasets, revealing kNN imputation’s consistent outperformance. This contribution adds valuable insights to the ongoing discourse on selecting optimal methods for handling missing data in data mining tasks. Furthermore, we introduce an additional validation layer by subjecting the imputed data to scrutiny through Long Short-Term Memory (LSTM) networks []. This not only assesses the accuracy of imputation but also gauges the temporal coherence of the imputed values.
By undertaking this exploration, we aim to contribute valuable insights into the realm of missing values imputation, offering a nuanced understanding of the capabilities of transformer-based models. The observed improvements in imputation accuracy, particularly validated through LSTM analysis, underscore the potential of our proposed approach to address the persistent challenges associated with missing data. Through this work, we aspire to provide a robust foundation for future advancements in data preprocessing and analysis methodologies. These are the key contributions of the article:
Handling missing values in datasets is a crucial challenge, particularly when predicting these values based on available data. Figure 1 outlines a comprehensive process for predicting missing values using a transformer model. In the initial step, we showcase an example dataset with missing values, highlighting the intricacies of the task. Moving to step two, we prepare the data for missing values imputation by segregating complete data for model training and reserving a test set for predicting missing data. Before arranging the data, each data sequence is assigned a unique identifier, ensuring traceability. Complete data features (f0, f3, f6, and f9) are repositioned on the right side in the third step. Subsequently, in step four, all complete rows are relocated to the top of the dataset.
Step five reveals the division of the dataset into X-data and Y-data, forming the basis for training the model. In step six, we select the complete X-Data and the target feature f1 from Y-Data, which contains missing data. Utilizing the train-test split on X-Data and Y-Data (f1), we generate X-Train, Y-Train, X-Test, and Y-Test. In step seven, the train data is prepared for our proposed prediction model, providing a complete set for training the Transformer model.
Advancing further, at step eight, the transformer undergoes comprehensive training using the entirety of the available data. In the subsequent step nine, the adeptly trained model takes on the task of predicting missing values within the X-Data. The imputed f1 feature is seamlessly integrated back into the X-Data, initiating a cascading effect as subsequent missing values are accurately predicted. This iterative refinement persists until the entirety of missing values is meticulously filled.
In the culminating step, the dataset is meticulously organized, preserving its inherent structure by adhering to initially assigned IDs. This methodical approach not only ensures the seamless integration of imputed values but also maintains the overall integrity and coherence of the dataset. In essence, our methodology provides a structured and systematic solution, navigating the intricacies of missing value imputation using a transformer model.
After the missing data imputation process finished using our suggested transformer-based prediction model, a thorough validation was carried out. During the validation stage, we aimed to assess how well our suggested model performed in comparison to other widely used imputation techniques, such as zero, mean, mode, and KNN imputation. We used these various imputation methods to produce five sets of imputed data. We validated each imputation model using Long Short-Term Memory (LSTM) networks to evaluate its effectiveness thoroughly. The LSTM network was fed the imputed data from all five models, including our suggested transformer-based imputation, as shown in Figure 2. Our objective was to conduct a comprehensive comparison and evaluation of the overall performance and forecast accuracy for each imputed dataset. Notably, the results consistently demonstrated the superior performance of our proposed transformer-based prediction-based imputation model when pitted against other, less intricate imputation techniques. This underscores its robust predictive capabilities in effectively managing missing values within the dataset.
The validation procedure, when juxtaposed with conventional imputation techniques, serves as a testament to the resilience and efficacy of our proposed model. The outcomes not only showcase its superiority but also affirm its ability to outperform fewer complex alternatives.
Table 1 examines the imputation performance across three datasets: hourly energy consumption data, daily energy consumption data, and monthly energy consumption data; the R2 score emerges as a critical metric for evaluating the effectiveness of various imputation methods. The proposed imputation model yields a noteworthy R2 score of 0.96 in hourly data, showcasing a substantial improvement of 0.195 over the next best method, KNN imputation. This enhancement underscores the proposed model’s ability to capture underlying patterns within the data, outshining traditional techniques such as zero, mean, and mode imputation. Similarly, the proposed model’s R2 score of 0.806 in daily data outperforms the KNN imputation by 0.015, demonstrating a notable superiority of 0.25 over the mean imputation. Moving to monthly data, the proposed model’s R2 score of 0.796 excels, showcasing a significant improvement of 0.1 over mean imputation and an even more substantial gain of 0.359 over mode imputation.
Overall, these results consistently highlight the proposed model’s effectiveness in preserving data relationships and capturing variability across diverse datasets, positioning it as a robust choice for imputing missing values when accurate modeling of underlying data patterns is crucial. A visual analysis of the r2 score for the selected imputation method is illustrated in Figure 3.
Beyond R2 scores, an in-depth analysis of other error metrics further solidifies the superiority of the proposed imputation model, as shown in Figure 4. In hourly consumption data, the model’s Mean Absolute Error (MAE) of 0.036 is notably lower than that of other methods, reflecting its ability to predict missing values with minimal deviation accurately. This trend continues in daily and monthly consumption data, where the proposed model consistently achieves the lowest MAE values, indicating superior imputation accuracy. Similarly, examining Mean Squared Error (MSE) and Root Mean Squared Error (RMSE) across all datasets, the proposed model consistently outperforms alternative methods. The observed reductions in MAE, MSE, and RMSE collectively underscore the robustness of the proposed model in minimizing imputation errors. These comprehensive findings suggest that, beyond R2 scores, the proposed imputation model consistently excels across various error metrics, affirming its efficacy in accurately filling missing data and offering a comprehensive solution for handling diverse datasets with absent values.
In this study, we have demonstrated the superior efficacy of transformer models over traditional methods like zero mean and KNN imputation, particularly in handling accuracy and context in missing data. However, the performance of these models varies with different data types and sizes, highlighting potential limitations in scalability and applicability to diverse datasets. Comparative analysis suggests that while transformers excel in interpreting sequential data, they may not be the most suitable choice for simpler or smaller datasets. The practical applications of our model are promising, yet they are accompanied by challenges in computational demands and ethical considerations, especially in sensitive sectors like healthcare and finance. The generalizability of our model across various types of missing data and its application across different fields remains an area ripe for further research and validation.
Future studies should focus on integrating advanced machine learning techniques to enhance the robustness and applicability of our model. Additionally, while the use of LSTM networks for validation is beneficial, alternative methods might provide a more comprehensive evaluation. It is crucial to acknowledge that the quality of imputation has a significant impact on the predictive accuracy of models, particularly in fields where data integrity is crucial. Our findings highlight the importance of continuous development in imputation methods, keeping pace with evolving data complexities and advancements in AI. This research contributes to the broader understanding of missing data imputation, setting a foundational stage for future innovations in predictive modeling.
This paper introduces a novel transformer-based prediction model to handle the critical problem of dataset missing value imputation. By methodically explaining the process, we demonstrated a comprehensive strategy that outperformed conventional imputation strategies, such as zero imputation, mean imputation, and KNN imputation. The suggested model demonstrated exceptional prediction powers by capturing complex patterns in sequential data. Our model significantly outperformed alternative imputation techniques after extensive validation using LSTM networks, highlighting its effectiveness and resilience. The present study significantly contributes to advancing missing values imputation approaches by providing a detailed comparative analysis of transformer-based and conventional methods. In light of the difficulties associated with missing data, the suggested approach closes a large gap in the literature and offers a viable path toward more trustworthy data analysis.
Du J, Hu M, Zhang W. Missing data problem in the monitoring system: A review. IEEE Sensors Journal. 2020; 20(23):13984-13998.
Alruhaymi AZ, Kim CJ. Study on the Missing Data Mechanisms and Imputation Methods. Open Journal of Statistics. 2021; 11(4):477-492.
Liu J, Pasumarthi S, Duffy B, Gong E, Datta K, Zaharchuk G. One Model to Synthesize Them All: Multi-Contrast Multi-Scale Transformer for Missing Data Imputation. IEEE Trans Med Imaging. 2023 Sep;42(9):2577-2591. doi: 10.1109/TMI.2023.3261707. Epub 2023 Aug 31. PMID: 37030684; PMCID: PMC10543020.
Edelman BL, Goel S, Kakade S, Zhang C. Inductive biases and variable creation in self-attention mechanisms. In International Conference on Machine Learning. PMLR. 2022; 5793-5831.
Choi SR, Lee M. Transformer Architecture and Attention Mechanisms in Genome Data Analysis: A Comprehensive Review. Biology (Basel). 2023 Jul 22;12(7):1033. doi: 10.3390/biology12071033. PMID: 37508462; PMCID: PMC10376273.
Schafer JL. Analysis of incomplete multivariate data. CRC press. 1997.
Menard S. Applied logistic regression analysis. Sage. 2002. 106.
Little RJ, Rubin DB. Statistical analysis with missing data. John Wiley & Sons. 2019; 793.
Hadeed SJ, O'Rourke MK, Burgess JL, Harris RB, Canales RA. Imputation methods for addressing missing data in short-term monitoring of air pollutants. Sci Total Environ. 2020 Aug 15;730:139140. doi: 10.1016/j.scitotenv.2020.139140. Epub 2020 May 3. PMID: 32402974; PMCID: PMC7745257.
Luo Y. Evaluating the state of the art in missing data imputation for clinical data. Brief Bioinform. 2022 Jan 17;23(1):bbab489. doi: 10.1093/bib/bbab489. PMID: 34882223; PMCID: PMC8769894.
Wang M, Gan J, Han C, Guo Y, Chen K, Shi YZ, Zhang BG. Imputation methods for scRNA sequencing data. Applied Sciences. 2022; 12(20):10684.
Samad T, Harp SA. Self–organization with partial data. Network: Computation in Neural Systems. 1992; 3(2):205-212.
Fessant F, Midenet S. Self-organising map for data imputation and correction in surveys. Neural Computing & Applications. 2002; 10:300-310.
Westin LK. Missing data and the preprocessing perceptron. Univ. 2004.
Sherwood B, Wang L, Zhou XH. Weighted quantile regression for analyzing health care cost data with missing covariates. Stat Med. 2013 Dec 10;32(28):4967-79. doi: 10.1002/sim.5883. Epub 2013 Jul 9. PMID: 23836597.
Crambes C, Henchiri Y. Regression imputation in the functional linear model with missing values in the response. Journal of Statistical Planning and Inference. 2019; 201:103-119.
Siswantining T, Soemartojo SM, Sarwinda D. Application of sequential regression multivariate imputation method on multivariate normal missing data. In 2019 3rd International Conference on Informatics and Computational Sciences (ICICoS). IEEE. 2019; 1-6.
Andridge RR, Little RJ. A Review of Hot Deck Imputation for Survey Non-response. Int Stat Rev. 2010 Apr;78(1):40-64. doi: 10.1111/j.1751-5823.2010.00103.x. PMID: 21743766; PMCID: PMC3130338.
Rubin LH, Witkiewitz K, Andre JS, Reilly S. Methods for Handling Missing Data in the Behavioral Neurosciences: Don't Throw the Baby Rat out with the Bath Water. J Undergrad Neurosci Educ. 2007 Spring;5(2):A71-7. Epub 2007 Jun 15. PMID: 23493038; PMCID: PMC3592650.
Rubin DB. Inference and missing data. Biometrika. 1976; 63(3):581-592.
Uusitalo L, Lehikoinen A, Helle I, Myrberg K. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environmental Modelling & Software. 2015; 63:24-31.
Kabir G, Tesfamariam S, Hemsing J, Sadiq R. Handling incomplete and missing data in water network database using imputation methods. Sustainable and Resilient Infrastructure. 2020; 5(6):365-377.
Yu L, Zhou R, Chen R, Lai KK. Missing data preprocessing in credit classification: One-hot encoding or imputation?. Emerging Markets Finance and Trade. 2022; 58(2):472-482.
Al-Helali B, Chen Q, Xue B, Zhang M. A new imputation method based on genetic programming and weighted KNN for symbolic regression with incomplete data. Soft Computing. 2021; 25:5993-6012.
Zhao Y, Long Q. Multiple imputation in the presence of high-dimensional data. Stat Methods Med Res. 2016 Oct;25(5):2021-2035. doi: 10.1177/0962280213511027. Epub 2013 Nov 25. PMID: 24275026.
Huque MH, Carlin JB, Simpson JA, Lee KJ. A comparison of multiple imputation methods for missing data in longitudinal studies. BMC Med Res Methodol. 2018 Dec 12;18(1):168. doi: 10.1186/s12874-018-0615-6. PMID: 30541455; PMCID: PMC6292063.
Horton NJ, Lipsitz SR, Parzen M. A potential for bias when rounding in multiple imputation. The American Statistician. 2003; 57(4):229-232.
Yi J, Lee J, Kim KJ, Hwang SJ, Yang E. Why not to use zero imputation? correcting sparsity bias in training neural networks. arXiv preprint arXiv:1906.00150. 2019.
Emmanuel T, Maupong T, Mpoeleng D, Semong T, Mphago B, Tabona O. A survey on missing data in machine learning. J Big Data. 2021;8(1):140. doi: 10.1186/s40537-021-00516-9. Epub 2021 Oct 27. PMID: 34722113; PMCID: PMC8549433.
Mohammed MB, Zulkafli HS, Adam MB, Ali N, Baba IA. Comparison of five imputation methods in handling missing data in a continuous frequency table. In AIP Conference Proceedings. AIP Publishing. 2021; 2355:1
Jadhav A, Pramod D, Ramanathan K. Comparison of performance of data imputation methods for numeric dataset. Applied Artificial Intelligence. 2019; 33(10):913-933.
Staudemeyer RC, Morris ER. Understanding LSTM--a tutorial into long short-term memory recurrent neural networks. arXiv preprint arXiv:1909.09586. 2019.
Ayub H, Jamil H. Enhancing Missing Values Imputation through Transformer-Based Predictive Modeling. IgMin Res. 23 Jan, 2024; 2(1): 025-031. IgMin ID: igmin140; DOI: 10.61927/igmin140; Available at: www.igminresearch.com/articles/pdf/igmin140.pdf
次のリンクを共有した人は、このコンテンツを読むことができます:
1Interdisciplinary Graduate Program in Advance Convergence Technology and Science, Jeju National University, Jeju, 63243, Republic of Korea
2Department of Electronics Engineering, Jeju National University, Jeju, 63243, Jeju-do, Republic of Korea
Address Correspondence:
Harun Jamil, Department of Electronics Engineering, Jeju National University, Jeju, 63243, Jeju-do, Republic of Korea, Email: [email protected]
How to cite this article:
Ayub H, Jamil H. Enhancing Missing Values Imputation through Transformer-Based Predictive Modeling. IgMin Res. 23 Jan, 2024; 2(1): 025-031. IgMin ID: igmin140; DOI: 10.61927/igmin140; Available at: www.igminresearch.com/articles/pdf/igmin140.pdf
Copyright: © 2024 Ayub H, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
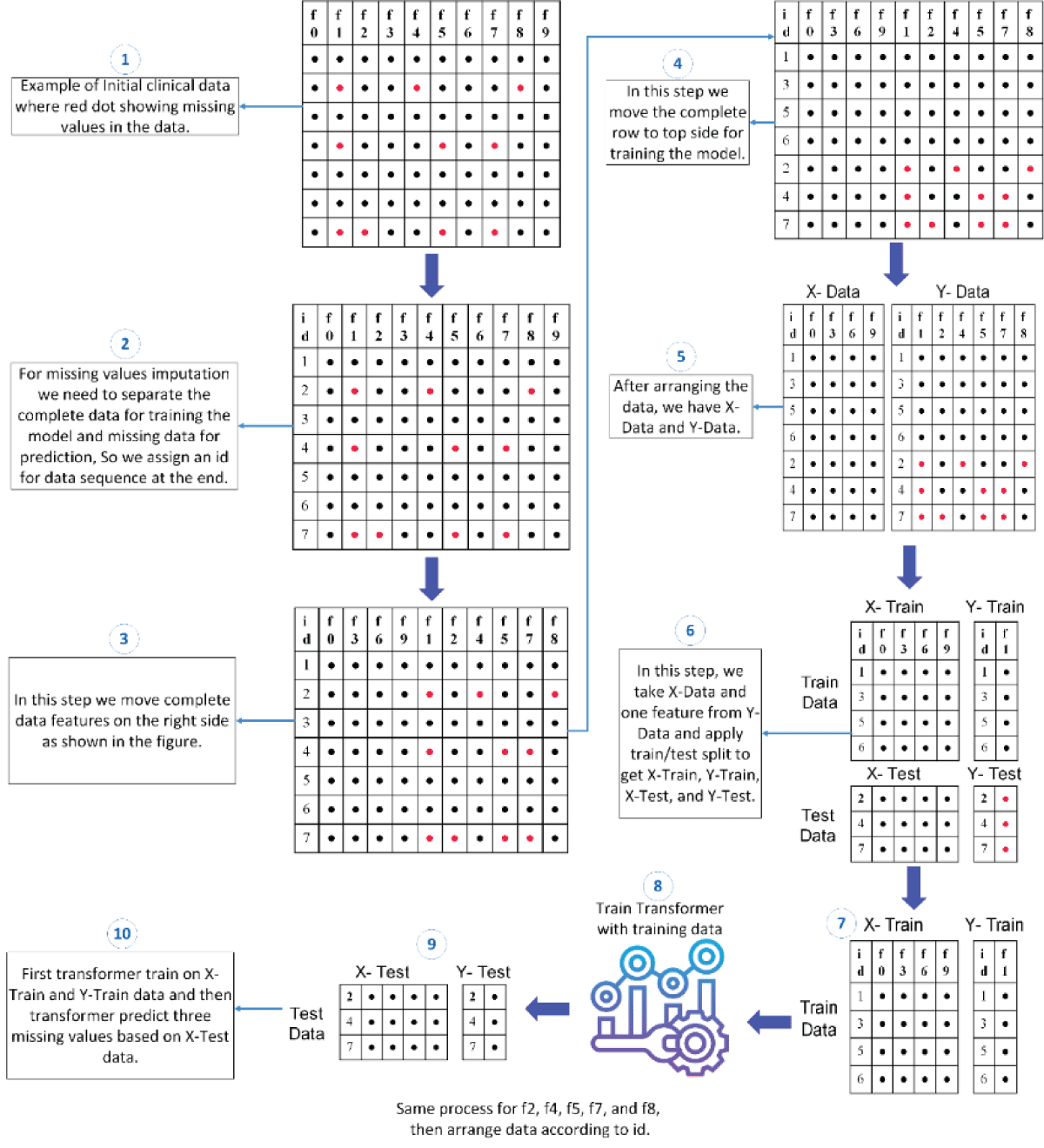 Figure 1: A detailed process of preparing data for the Trans...
Figure 1: A detailed process of preparing data for the Trans...
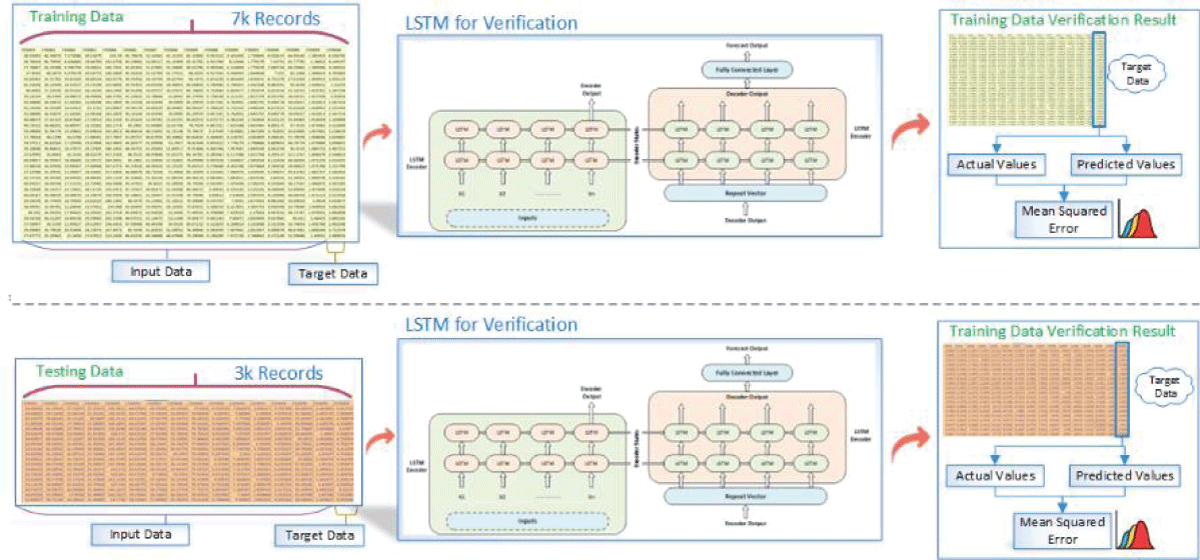 Figure 2: Validation process of the Imputed data using LSTM....
Figure 2: Validation process of the Imputed data using LSTM....
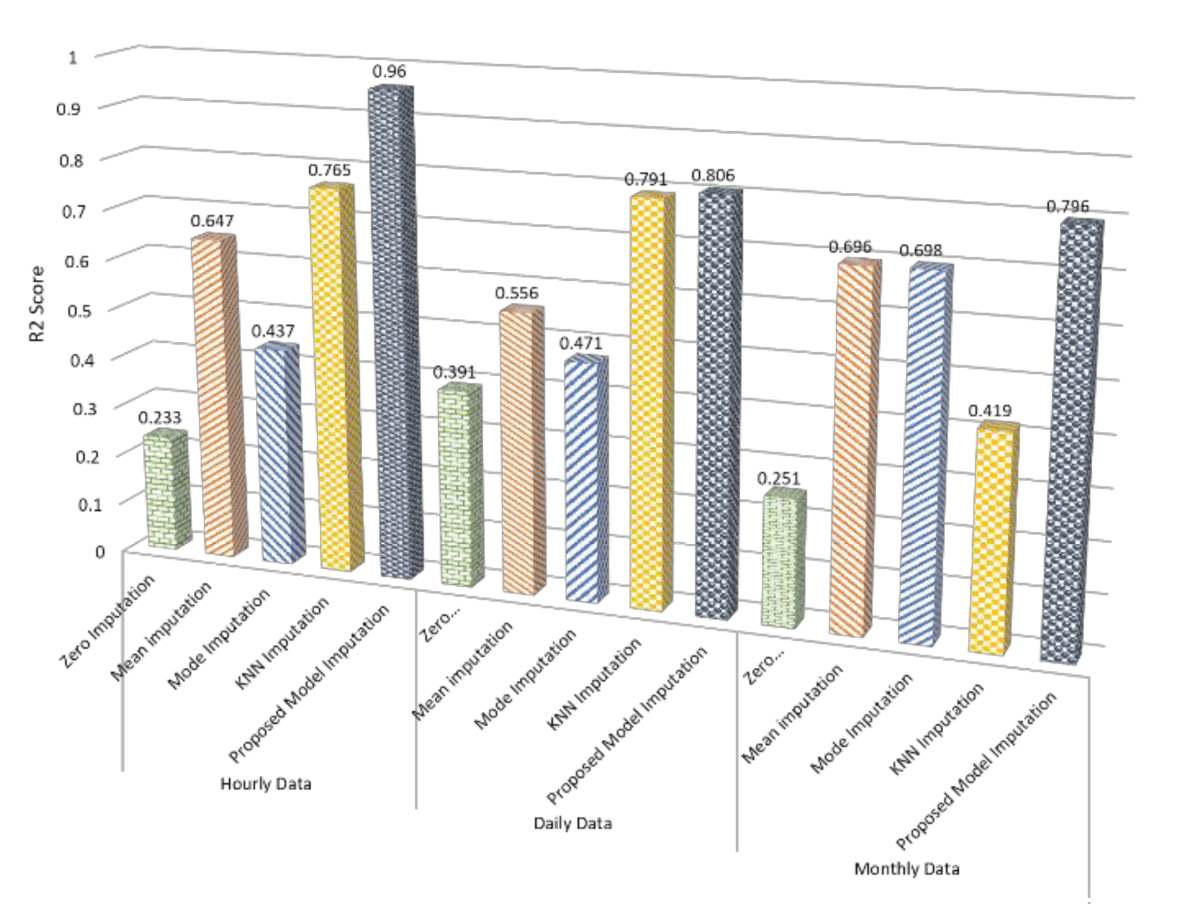 Figure 3: R2 score analysis for the selected imputation meth...
Figure 3: R2 score analysis for the selected imputation meth...
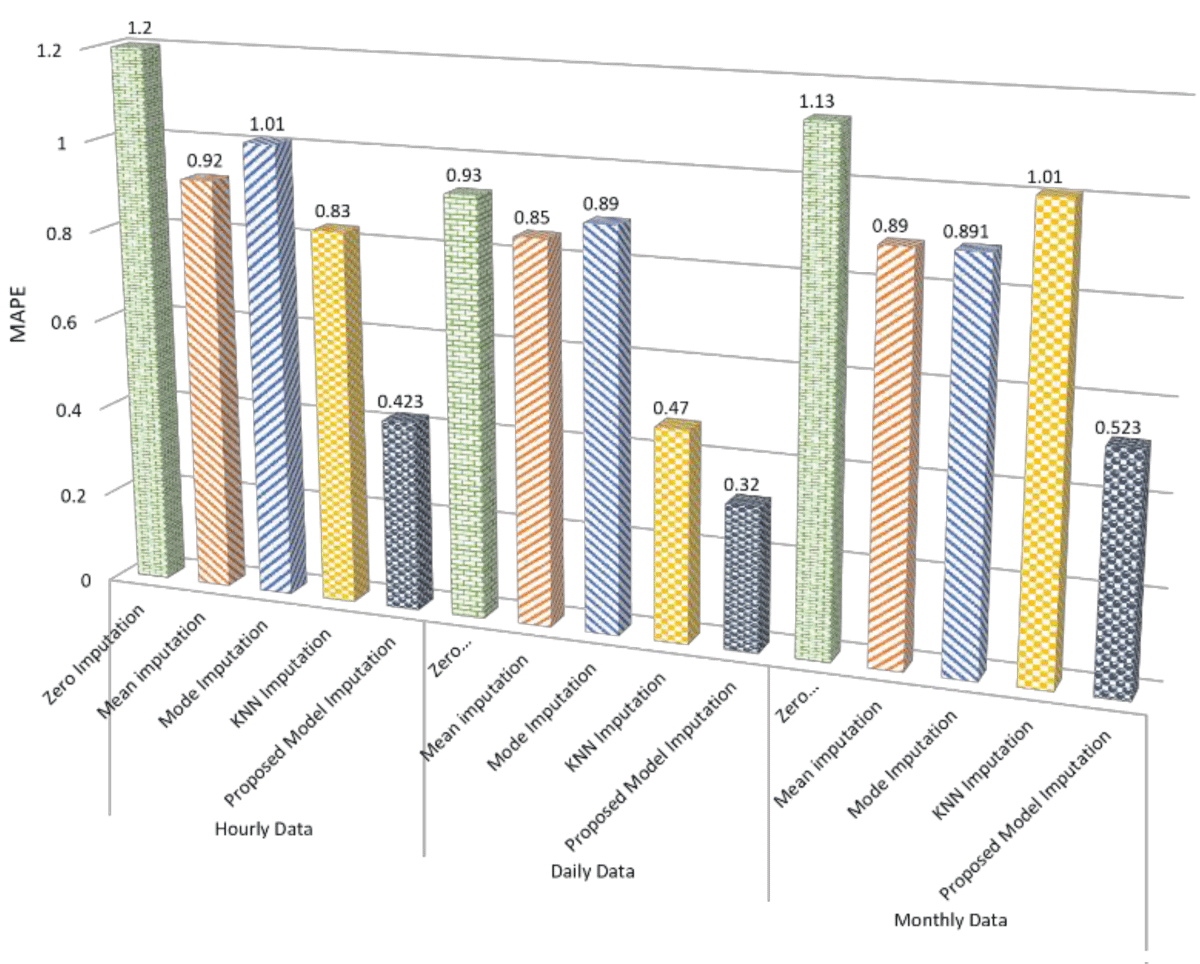 Figure 4: MAPE analysis for the selected imputation methods....
Figure 4: MAPE analysis for the selected imputation methods....
 Table 1: A detailed comparative analysis of the Imputation ...
Table 1: A detailed comparative analysis of the Imputation ...
Du J, Hu M, Zhang W. Missing data problem in the monitoring system: A review. IEEE Sensors Journal. 2020; 20(23):13984-13998.
Alruhaymi AZ, Kim CJ. Study on the Missing Data Mechanisms and Imputation Methods. Open Journal of Statistics. 2021; 11(4):477-492.
Liu J, Pasumarthi S, Duffy B, Gong E, Datta K, Zaharchuk G. One Model to Synthesize Them All: Multi-Contrast Multi-Scale Transformer for Missing Data Imputation. IEEE Trans Med Imaging. 2023 Sep;42(9):2577-2591. doi: 10.1109/TMI.2023.3261707. Epub 2023 Aug 31. PMID: 37030684; PMCID: PMC10543020.
Edelman BL, Goel S, Kakade S, Zhang C. Inductive biases and variable creation in self-attention mechanisms. In International Conference on Machine Learning. PMLR. 2022; 5793-5831.
Choi SR, Lee M. Transformer Architecture and Attention Mechanisms in Genome Data Analysis: A Comprehensive Review. Biology (Basel). 2023 Jul 22;12(7):1033. doi: 10.3390/biology12071033. PMID: 37508462; PMCID: PMC10376273.
Schafer JL. Analysis of incomplete multivariate data. CRC press. 1997.
Menard S. Applied logistic regression analysis. Sage. 2002. 106.
Little RJ, Rubin DB. Statistical analysis with missing data. John Wiley & Sons. 2019; 793.
Hadeed SJ, O'Rourke MK, Burgess JL, Harris RB, Canales RA. Imputation methods for addressing missing data in short-term monitoring of air pollutants. Sci Total Environ. 2020 Aug 15;730:139140. doi: 10.1016/j.scitotenv.2020.139140. Epub 2020 May 3. PMID: 32402974; PMCID: PMC7745257.
Luo Y. Evaluating the state of the art in missing data imputation for clinical data. Brief Bioinform. 2022 Jan 17;23(1):bbab489. doi: 10.1093/bib/bbab489. PMID: 34882223; PMCID: PMC8769894.
Wang M, Gan J, Han C, Guo Y, Chen K, Shi YZ, Zhang BG. Imputation methods for scRNA sequencing data. Applied Sciences. 2022; 12(20):10684.
Samad T, Harp SA. Self–organization with partial data. Network: Computation in Neural Systems. 1992; 3(2):205-212.
Fessant F, Midenet S. Self-organising map for data imputation and correction in surveys. Neural Computing & Applications. 2002; 10:300-310.
Westin LK. Missing data and the preprocessing perceptron. Univ. 2004.
Sherwood B, Wang L, Zhou XH. Weighted quantile regression for analyzing health care cost data with missing covariates. Stat Med. 2013 Dec 10;32(28):4967-79. doi: 10.1002/sim.5883. Epub 2013 Jul 9. PMID: 23836597.
Crambes C, Henchiri Y. Regression imputation in the functional linear model with missing values in the response. Journal of Statistical Planning and Inference. 2019; 201:103-119.
Siswantining T, Soemartojo SM, Sarwinda D. Application of sequential regression multivariate imputation method on multivariate normal missing data. In 2019 3rd International Conference on Informatics and Computational Sciences (ICICoS). IEEE. 2019; 1-6.
Andridge RR, Little RJ. A Review of Hot Deck Imputation for Survey Non-response. Int Stat Rev. 2010 Apr;78(1):40-64. doi: 10.1111/j.1751-5823.2010.00103.x. PMID: 21743766; PMCID: PMC3130338.
Rubin LH, Witkiewitz K, Andre JS, Reilly S. Methods for Handling Missing Data in the Behavioral Neurosciences: Don't Throw the Baby Rat out with the Bath Water. J Undergrad Neurosci Educ. 2007 Spring;5(2):A71-7. Epub 2007 Jun 15. PMID: 23493038; PMCID: PMC3592650.
Rubin DB. Inference and missing data. Biometrika. 1976; 63(3):581-592.
Uusitalo L, Lehikoinen A, Helle I, Myrberg K. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environmental Modelling & Software. 2015; 63:24-31.
Kabir G, Tesfamariam S, Hemsing J, Sadiq R. Handling incomplete and missing data in water network database using imputation methods. Sustainable and Resilient Infrastructure. 2020; 5(6):365-377.
Yu L, Zhou R, Chen R, Lai KK. Missing data preprocessing in credit classification: One-hot encoding or imputation?. Emerging Markets Finance and Trade. 2022; 58(2):472-482.
Al-Helali B, Chen Q, Xue B, Zhang M. A new imputation method based on genetic programming and weighted KNN for symbolic regression with incomplete data. Soft Computing. 2021; 25:5993-6012.
Zhao Y, Long Q. Multiple imputation in the presence of high-dimensional data. Stat Methods Med Res. 2016 Oct;25(5):2021-2035. doi: 10.1177/0962280213511027. Epub 2013 Nov 25. PMID: 24275026.
Huque MH, Carlin JB, Simpson JA, Lee KJ. A comparison of multiple imputation methods for missing data in longitudinal studies. BMC Med Res Methodol. 2018 Dec 12;18(1):168. doi: 10.1186/s12874-018-0615-6. PMID: 30541455; PMCID: PMC6292063.
Horton NJ, Lipsitz SR, Parzen M. A potential for bias when rounding in multiple imputation. The American Statistician. 2003; 57(4):229-232.
Yi J, Lee J, Kim KJ, Hwang SJ, Yang E. Why not to use zero imputation? correcting sparsity bias in training neural networks. arXiv preprint arXiv:1906.00150. 2019.
Emmanuel T, Maupong T, Mpoeleng D, Semong T, Mphago B, Tabona O. A survey on missing data in machine learning. J Big Data. 2021;8(1):140. doi: 10.1186/s40537-021-00516-9. Epub 2021 Oct 27. PMID: 34722113; PMCID: PMC8549433.
Mohammed MB, Zulkafli HS, Adam MB, Ali N, Baba IA. Comparison of five imputation methods in handling missing data in a continuous frequency table. In AIP Conference Proceedings. AIP Publishing. 2021; 2355:1
Jadhav A, Pramod D, Ramanathan K. Comparison of performance of data imputation methods for numeric dataset. Applied Artificial Intelligence. 2019; 33(10):913-933.
Staudemeyer RC, Morris ER. Understanding LSTM--a tutorial into long short-term memory recurrent neural networks. arXiv preprint arXiv:1909.09586. 2019.