Exploring Markov Decision Processes: A Comprehensive Survey of Optimization Applications and Techniques

Qazi Waqas Khan

doi:10.61927/igmin210

98 of 162

Contamination in Heat Exchangers: Types, Energy Effects and Prevention Methods

Mehmet Akif Kartal

100 of 162

A Machine Learning-based Method for COVID-19 and Pneumonia Detection

Qazi Waqas Khan

Engineering Group Review Article 記事ID: igmin210

Exploring Markov Decision Processes: A Comprehensive Survey of Optimization Applications and Techniques

Machine Learning Robotics DOI10.61927/igmin210

Qazi Waqas Khan ^*

Affiliation

Qazi Waqas Khan, Department of Computer Engineering, Jeju National University, Jejusi 63243, Jeju Special Self-Governing Province, Republic of Korea, Email: waqasqazi19@stu.jejunu.ac.kr

Fulltext HTML Fulltext PDF Cite this article

0

REFERENCES

1.3k

VIEWS

405

DOWNLOADS

128

要約

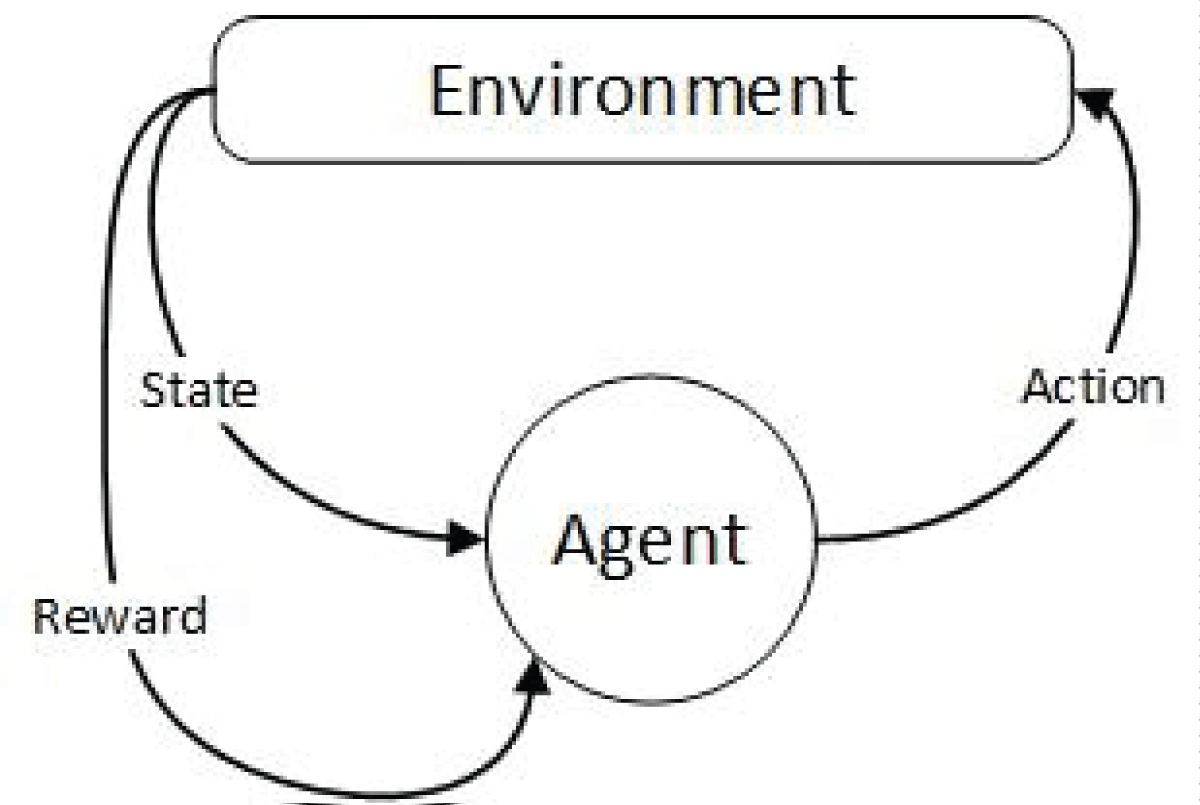
Markov decision process is a dynamic programming algorithm that can be used to solve an optimization problem. It was used in applications like robotics, radar tracking, medical treatments, and decision-making. In the existing literature, the researcher only targets a few applications area of MDP. However, this work surveyed the Markov decision process’s application in various regions for solving optimization problems. In a survey, we compared optimization techniques based on MDP. We performed a comparative analysis of past work of other researchers in the last few years based on a few parameters. These parameters are focused on the proposed problem, the proposed methodology for solving an optimization problem, and the results and outcomes of the optimization technique in solving a specific problem. Reinforcement learning is an emerging machine learning domain based on the Markov decision process. In this work, we conclude that the MDP-based approach is most widely used when deciding on the current state in some environments to move to the next state.

数字

参考文献

Goyal V, Grand-Clement J. Robust Markov decision processes: Beyond rectangularity. Math Oper Res. 2023;48(1):203-26. Available from: https://dl.acm.org/doi/10.1287/moor.2022.1259
Alsheikh MA, Lin S, Niyato D, Tan HP, Han Z. Markov decision processes with applications in wireless sensor networks: A survey. IEEE Commun Surv Tutor. 2015;17(3):1239-67. Available from: https://arxiv.org/abs/1501.00644
Bazrafshan N, Lotfi MM. A finite-horizon Markov decision process model for cancer chemotherapy treatment planning: an application to sequential treatment decision making in clinical trials. Ann Oper Res. 2020;295(1):483-502. Available from: https://ideas.repec.org/a/spr/annopr/v295y2020i1d10.1007_s10479-020-03706-5.html
Yao Q, Guo X, Wang Y, Liang H, Wu K. Adversarial decision-making for moving target defense: a multi-agent Markov game and reinforcement learning approach. Entropy. 2023;25(4):605. Available from: https://pubmed.ncbi.nlm.nih.gov/37190393/
Zheng J. Optimal policy for dynamically changing system controls in moving target defense [dissertation]. 2020. Available from: https://ttu-ir.tdl.org/items/26335752-875d-4219-a0eb-795dd653bf78
Zhang SP, Suen SC, Sundaram V, Gong CL. Quantifying the benefits of increasing decision-making frequency for health applications with regular decision epochs. IISE Trans. 2024:1-15. Available from: https://www.tandfonline.com/doi/pdf/10.1080/24725854.2024.2321492
Bozkus T, Mitra U. Link analysis for solving multiple-access MDPs with large state spaces. IEEE Trans Signal Process. 2023;71:947-62. Available from: https://ieeexplore.ieee.org/document/10078382/authors#authors
Xu Z, Song Z, Shrivastava A. A tale of two efficient value iteration algorithms for solving linear MDPs with large action space. In: International Conference on Artificial Intelligence and Statistics. PMLR; 2023;206:788-836. Available from: https://proceedings.mlr.press/v206/xu23b.html
Ghatrani Z, Ghate A. Inverse Markov decision processes with unknown transition probabilities. IISE Trans. 2023;55(6):588-601. Available from: https://www.tandfonline.com/doi/full/10.1080/24725854.2022.2103755
Low SM, Kumar A, Sanner S. Safe MDP planning by learning temporal patterns of undesirable trajectories and averting negative side effects. In: Proceedings of the International Conference on Automated Planning and Scheduling. 2023;33(1). Available from: https://doi.org/10.48550/arXiv.2304.03081
Wang Y, Xu Z, Liu Y, Chen X, Qiu S, Yu Y. Robust average-reward Markov decision processes. In: Proceedings of the AAAI Conference on Artificial Intelligence. 2023;37(12): AAAI-23 Special Tracks. Available from: https://doi.org/10.1609/aaai.v37i12.26775
Valeev S, Kondratyeva N. Large scale system management based on Markov decision process and big data concept. In: 2016 IEEE 10th International Conference on Application of Information and Communication Technologies (AICT). IEEE; 2016. Available from: https://ieeexplore.ieee.org/document/7991829
Winder J. Concept-aware feature extraction for knowledge transfer in reinforcement learning. In: AAAI Workshops. 2018. Available from: https://cdn.aaai.org/ocs/ws/ws0470/16910-76005-1-PB.pdf
Johnson FA, Fackler PL, Boomer GS, Zimmerman GS, Williams BK, Nichols JD, et al. State-dependent resource harvesting with lagged information about system states. PLoS One. 2016;11(6). Available from: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0157494
Pourmoayed R, Nielsen LR, Kristensen AR. A hierarchical Markov decision process modeling feeding and marketing decisions of growing pigs. Eur J Oper Res. 2016;250(3):925-938. Available from: https://www.sciencedirect.com/science/article/abs/pii/S0377221715008802
Morato PG, Papakonstantinou KG, Andriotis CP, Nielsen JS, Rigo P. Optimal inspection and maintenance planning for deteriorating structures through dynamic Bayesian networks and Markov decision processes. 2021. Available from: https://arxiv.org/abs/2009.04547
Boucherie RJ, Van Dijk NM. Markov decision processes in practice. Switzerland: Springer; 2017;248. Available from: https://research.utwente.nl/en/publications/markov-decision-processes-in-practice
Butkova Y, Hatefi H, Hermanns H, Krcal J. Optimal continuous time Markov decisions. In: International Symposium on Automated Technology for Verification and Analysis. Springer, Cham; 2015. Available from: https://arxiv.org/abs/1507.02876
Van Heerde HJ, Neslin SA. Sales promotion models. In: Handbook of Marketing Decision Models. Springer, Cham; 2017;13-77. Available from: https://ideas.repec.org/h/spr/isochp/978-3-319-56941-3_2.html
Zhang Z, Tian Y. A novel resource scheduling method of netted radars based on Markov decision process during target tracking in clutter. EURASIP J Adv Signal Process. 2016;2016:9. Available from: https://www.infona.pl/resource/bwmeta1.element.springer-doi-10_1186-S13634-016-0309-3
Conesa D, Martínez-Beneito MA, Amorós R, López-Quílez A. Bayesian hierarchical Poisson models with a hidden Markov structure for the detection of influenza epidemic outbreaks. Stat Methods Med Res. 2015 Apr;24(2):206-23. Available from: https://pubmed.ncbi.nlm.nih.gov/21873301/
Cheung WC, Simchi-Levi D, Zhu R. Reinforcement learning for non-stationary Markov decision processes: The blessing of (more) optimism. 2020. Available from: https://arxiv.org/abs/2006.14389
Killian T, Konidaris G, Doshi-Velez F. Transfer learning across patient variations with hidden parameter Markov decision processes. 2016. Available from: https://arxiv.org/pdf/1612.00475
Geist M, Scherrer B, Pietquin O. A theory of regularized Markov decision processes. 2019. Available from: https://arxiv.org/abs/1901.11275
Wei CY, Jafarnia-Jahromi M, Luo H, Sharma H, Jain R. Model-free reinforcement learning in infinite-horizon average-reward Markov decision processes. 2019. Available from: https://arxiv.org/abs/1910.07072
Wachi A, Sui Y. Safe reinforcement learning in constrained Markov decision processes. 2020. Available from: https://arxiv.org/abs/2008.06626
Lim SH, Xu H, Mannor S. Reinforcement learning in robust Markov decision processes. Math Oper Res. 2016;41(4):1325-53. Available from: https://pubsonline.informs.org/doi/abs/10.1287/moor.2016.0779
Le TP, Vien NA, Chung TC. A deep hierarchical reinforcement learning algorithm in partially observable Markov decision processes. IEEE Access. 2018;6:49089-102. Available from: https://ieeexplore.ieee.org/document/8421749
Modi A, Tewari A. Contextual Markov decision processes using generalized linear models. 2019. Available from: https://openreview.net/pdf?id=Bklh0SiQiN
Lee K, Choi S, Oh S. Sparse Markov decision processes with causal sparse Tsallis entropy regularization for reinforcement learning. 2017. Available from: https://arxiv.org/abs/1709.06293
Ding T, Zeng Z, Bai J, Qin B, Yang Y, Shahidehpour M. Optimal electric vehicle charging strategy with Markov decision process and reinforcement learning technique. IEEE Trans Ind Appl. 2020;56(5):5811-23. Available from: https://vbn.aau.dk/ws/portalfiles/portal/331224034/final.pdf
Wang Z, Qiu S, Wei X, Yang Z, Ye J. Upper confidence primal-dual reinforcement learning for CMDP with adversarial loss. In: Adv Neural Inf Process Syst. 2020;33. Available from: https://arxiv.org/abs/2003.00660
Wei Z, Xu J, Lan Y, Guo J, Cheng X. Reinforcement learning to rank with Markov decision process. In: Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval; 2017:945-948. Available from: https://dl.acm.org/doi/10.1145/3077136.3080685
Selvi E, Buehrer RM, Martone A, Sherbondy K. On the use of Markov decision processes in cognitive radar: An application to target tracking. In: 2018 IEEE Radar Conference (RadarConf18). IEEE; 2018. Available from: https://ieeexplore.ieee.org/document/8378616
Ruan A, Shi A, Qin L, Xu S, Zhao Y. A reinforcement learning-based Markov-Decision Process (MDP) implementation for SRAM FPGAs. IEEE Trans Circuits Syst. 2020;67:2124-2128. Available from: https://ieeexplore.ieee.org/document/8850046
De Giacomo G, Calvanese D, Dalmonte T, De Masellis R, Orsi G. Digital twin composition in smart manufacturing via Markov decision processes. Comput Ind. 2023;149:103916. Available from: https://www.sciencedirect.com/science/article/pii/S0166361523000660
Rosenberg A, Mansour Y. Online convex optimization in adversarial Markov decision processes. 2019. Available from: https://arxiv.org/abs/1905.07773
Chen CT, Chen AP, Huang SH. Cloning strategies from trading records using agent-based reinforcement learning algorithm. In: 2018 IEEE International Conference on Agents (ICA); 2018 Jul; IEEE. p. 34-37. Available from: https://ieeexplore.ieee.org/document/8460078
Archibald TW, Possani E. Investment and operational decisions for start-up companies: a game theory and Markov decision process approach. Ann Oper Res. 2019:1-14.
Bai Y, Meng J, Meng F, Fang G. Stochastic analysis of a shale gas investment strategy for coping with production uncertainties. Energy Policy. 2020;144:111639. Available from: https://ideas.repec.org/a/eee/enepol/v144y2020ics0301421520303748.html
Nasir A, Khursheed A, Ali K, Mustafa F. A Markov Decision Process Model for Optimal Trade of Options Using Statistical Data. Comput Econ. 2020;58:327-346. Available from: https://link.springer.com/article/10.1007/s10614-020-10030-4
Hambly B, Xu R, Yang H. Recent advances in reinforcement learning in finance. Math Finance. 2023;33(3):437-503. Available from: https://onlinelibrary.wiley.com/doi/epdf/10.1111/mafi.12382
Huong TT, Thanh NH, Van NT, Dat NT, Van Long N, Marshall A. Water and energy-efficient irrigation based on Markov decision model for precision agriculture. In: 2018 IEEE Seventh International Conference on Communications and Electronics (ICCE); 2018 Jul; IEEE. p. 51-56. Available from: https://ieeexplore.ieee.org/document/8465723
Bu F, Wang X. A smart agriculture IoT system based on deep reinforcement learning. Future Gener Comput Syst. 2019;99:500-507. Available from: https://typeset.io/papers/a-smart-agriculture-iot-system-based-on-deep-reinforcement-226i9iipdo?citations_has_pdf=true
Toai TK, Huan VM. Implementing the Markov Decision Process for Efficient Water Utilization with Arduino Board in Agriculture. In: 2019 International Conference on System Science and Engineering (ICSSE); 2019 Jul; IEEE. p. 335-340. Available from: https://ieeexplore.ieee.org/document/8823432
Pan W, Wang J, Yang W. A cooperative scheduling based on deep reinforcement learning for multi-agricultural machines in emergencies. Agriculture. 2024;14(5):772. Available from: https://www.mdpi.com/2077-0472/14/5/772
Liu D, Khoukhi L, Hafid A. Data offloading in mobile cloud computing: A Markov decision process approach. In: 2017 IEEE International Conference on Communications (ICC); 2017 May; IEEE. p. 1-6. Available from: https://ieeexplore.ieee.org/document/7997070
Li M, Carter A, Goldstein J, Hawco T, Jensen J, Vanberkel P. Determining Ambulance Destinations When Facing Offload Delays Using a Markov Decision Process. Omega. 2021;101:102251. Available from: https://www.sciencedirect.com/science/article/abs/pii/S0305048319308229
Parras J, Zazo S. Learning attack mechanisms in wireless sensor networks using Markov decision processes. Expert Syst Appl. 2019;122:376-387. Available from: https://www.sciencedirect.com/science/article/abs/pii/S0957417419300235
Li X, Fang Z, Yin C. A machine tool matching method in cloud manufacturing using Markov Decision Process and cross-entropy. Robot Comput Integr Manuf. 2020;65:101968. Available from: https://www.sciencedirect.com/science/article/abs/pii/S0736584519300924
Li Z. An adaptive overload threshold selection process using Markov decision processes of virtual machine in cloud data center. Clust Comput. 2019;22(2):3821-3833. Available from: https://link.springer.com/article/10.1007/s10586-018-2408-4
Yousefi S, Derakhshan F, Karimipour H, Aghdasi HS. An efficient route planning model for mobile agents on the Internet of Things using Markov decision process. Ad Hoc Netw. 2020;98:102053. Available from: https://www.sciencedirect.com/science/article/abs/pii/S1570870519309527
Njilla LL, Kamhoua CA, Kwiat KA, Hurley P, Pissinou N. Cyber security resource allocation: a Markov decision process approach. In: 2017 IEEE 18th International Symposium on High Assurance Systems Engineering (HASE); 2017 Jan; IEEE. p. 49-52. Available from: https://ieeexplore.ieee.org/abstract/document/7911870/
Chitsaz B, Cosenza B, Gupta V, Thain D, Mackay S. Scaling power management in cloud data centers: A multi-level continuous-time MDP approach. IEEE Trans Serv Comput. 2024;1-12. Available from: https://ieeexplore.ieee.org/abstract/document/10400800
Duan J, Lv C, Xing Y, Du H, Cheng B, Sangiovanni-Vincentelli AL. Hierarchical reinforcement learning for self-driving decision-making without reliance on labeled driving data. IET Intell Transp Syst. 2020;14(5):297-305. Available from: https://ietresearch.onlinelibrary.wiley.com/doi/full/10.1049/iet-its.2019.0317
Kamrani M, Rakha H, Ma Y. Applying Markov decision process to understand driving decisions using basic safety messages data. Transp Res Part C Emerg Technol. 2020;115:102642. Available from: https://www.sciencedirect.com/science/article/abs/pii/S0968090X20305490
Qi X, Jiang R, Li K, Wang W, Qi J. Deep reinforcement learning enabled self-learning control for energy-efficient driving. Transp Res Part C Emerg Technol. 2019;99:67-81. Available from: https://www.sciencedirect.com/science/article/abs/pii/S0968090X18318862
Ghosh S, Topcu U, Chong E, Etigowni S, Fainekos G, Kakade U. Model, data and reward repair: Trusted machine learning for Markov Decision Processes. In: 2018 48th Annual IEEE/IFIP International Conference on Dependable Systems and Networks Workshops (DSN-W); 2018; IEEE. Available from: https://ieeexplore.ieee.org/abstract/document/8416249
Song Y, Han S, Huh K. A self-driving decision making with reachable path analysis and interaction-aware speed profiling. IEEE Access. 2023;11:122302-122314. Available from: https://ieeexplore.ieee.org/abstract/document/10301421
de Almeida Costa M, de Azevedo Peixoto Braga JP, Ramos Andrade A. A data-driven maintenance policy for railway wheelsets based on survival analysis and Markov decision process. Qual Reliab Eng Int. 2021;37:176-198. Available from:
Ao Y, Zhang H, Wang C. Research of an integrated decision model for production scheduling and maintenance planning with economic objectives. Comput Ind Eng. 2019;137:106092. Available from: https://www.sciencedirect.com/science/article/abs/pii/S0360835219305613
Gerum PCL, Altay A, Baykal-Gürsoy M. Data-driven predictive maintenance scheduling policies for railways. Transp Res Part C Emerg Technol. 2019;107:137-154. Available from: https://www.sciencedirect.com/science/article/abs/pii/S0968090X18314918
Arcieri G, Masegosa AD, Stella F, Vercellis C. POMDP inference and robust solution via deep reinforcement learning: An application to railway optimal maintenance. Mach Learn. 2024:1-29. Available from: https://link.springer.com/article/10.1007/s10994-024-06559-2

類似の記事

Influence of Polycarboxylate Superplasticizer on the Calorimetric and Physicomechanical Properties of Mortar
Alya Harichane and Fatiha Belalia
DOI10.61927/igmin128

The Model for Clinical, Laboratory, and Genetic Prediction of Recurrent Ischemic Stroke against the Background of Laboratory Aspirin Resistance using Machine Learning
Anastasia V Anisimova, Sergey S Galkin, Anastasia S Gunchenko, Tatyana V Nasedkina and Igor V Vorobiev
DOI10.61927/igmin143

Fibrin Contributes to an Improvement of an in vitro Wound Repair Model using Fibroblast-populated Collagen Lattices
Mario Chopin-Doroteo, Aldo Montes de Oca-Delgado, Rosa M Salgado and Edgar Krötzsch
DOI10.61927/igmin159

Cyber Threat Analysis (CTA) in Current Conflicts
Zbigniew Ciekanowski and Sławomir Żurawski
DOI10.61927/igmin169

Development of a Mechanical Seal Closed Design Model
Serhii Shevchenko
DOI10.61927/igmin152

Analysis of Reliable Transmission Performance Optimization Methods for Satellite-to-Ground Laser Communication Links
Zhi Liu, Qingfang Jiang, Kanglian Zhao, Xianzhu Liu, Wanzhuo Ma and Xiaolong Ni
DOI10.61927/igmin230

Analysis of Damages to Boiler Screen Tubes BKZ-160-100-GM (Barnaul Boiler Plant, steam productivity 160 t/h, pressure 100 kgf/cm2, Fuel: Natural Gas/Fuel Oil) after Reconstruction for Increased Steam Productivity to 210 t/h
MS Popov, II Belyakov and AD Tolstyh
DOI10.61927/igmin168

Quantum Perception and Quantum Computation
MV Takook
DOI10.61927/igmin253

EB Naevi-like Lesion in Infant Bullous Pemphigoid
Laura Serpa, Haizza Monteiro, Maria de Oliveira Buffara, Raíssa Rodriguez, Ana Luisa Alves, Viviane Maria Maiolini and Elisa Fontenelle*
DOI10.61927/igmin201

LC-MS and HPLC-UV for Detecting Uremic Toxins: Two Validated Methods with Simultaneous Sensitivity and Specificity Evaluation
Cristina Filosa
DOI10.61927/igmin175